题目内容
10．若无理数$\sqrt{2a-9}$与-$\sqrt{a-3}$为正数m的平方根，则m=3．分析 根据一个正数有两个平方根，这两个平方根互为相反数，可得$\sqrt{2a-9}$=$\sqrt{a-3}$，然后去掉根号，求出a的值是多少，进而求出a-3的值是多少，即可确定m的值是多少．
解答 解：∵无理数$\sqrt{2a-9}$与-$\sqrt{a-3}$为正数m的平方根，
∴$\sqrt{2a-9}$=$\sqrt{a-3}$，
∴2a-9=a-3，
解得a=6，
所以m=${（-\sqrt{6-3}）}^{2}$=3．
故答案为：3．
点评 此题主要考查了平方根的性质和应用，要熟练掌握，解答此题的关键是要明确：一个正数有两个平方根，这两个平方根互为相反数．
练习册系列答案
相关题目
8．体育文化用品店购进篮球和排球共40个，进价和售价如表，全部售完后共获利520元．
（1）购进篮球和排球各多少个？
（2）销售时，用6000元买了50个篮球和若干个排球，能获得利润多少？
| 篮球 | 排球 | |
| 进价（元/个） | 80 | 50 |
| 售价（元/个） | 95 | 60 |
（2）销售时，用6000元买了50个篮球和若干个排球，能获得利润多少？
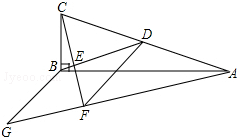如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若FG=5，CF=6，则四边形BDFG的面积为15．