题目内容
8. 如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC交⊙O于点D,直线CD交BA的延长线于点E.求证:CD为⊙O的切线.
如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC交⊙O于点D,直线CD交BA的延长线于点E.求证:CD为⊙O的切线.
分析 由切线的性质得∠CBO=90°,首先连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线.
解答 证明:连结DO.
∵AB为⊙O的直径,BC为⊙O的切线,
∴∠CBO=90°,
∵AD∥OC,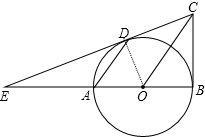
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中,
$\left\{\begin{array}{l}{CO=DO}\\{∠COD=∠COB}\\{OD=OB}\end{array}\right.$,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO=90°.
又∵点D在⊙O上,
∴CD是⊙O的切线.
点评 本题主要考查了切线的判定、全等三角形的判定与性质以及相似三角形的判定与性质,注意掌握辅助线的作法,注意数形结合思想的应用是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下面是某同学做的三道题:
(1)若x2=4,则x=2;
(2)方程2x(x-1)=(x-1)的解为x=0;
(3)方程x2-8x+2=0的两根之和为2.
其中答案完全正确的题目个数为( )
(1)若x2=4,则x=2;
(2)方程2x(x-1)=(x-1)的解为x=0;
(3)方程x2-8x+2=0的两根之和为2.
其中答案完全正确的题目个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.对于二次函数y=x2-2x+4,下列说法正确的是( )
| A. | 抛物线的对称轴是直线x=1,顶点坐标是(1,3) | |
| B. | 由于抛物线的开口向上,所以y随x的增大而减小 | |
| C. | 抛物线与x轴肯定有交点 | |
| D. | 这个二次函数的值既可以大于零,也可以小于零 |
13.以下事件中,必然发生的是( )
| A. | 打开电视机,正在播放体育节目 | B. | 正五边形的外角和为180° | ||
| C. | 掷一次骰子,向上一面是5点 | D. | 通常情况下,水加热到100℃沸腾 |
18.一元二次方程x2-2x-1=0的二次项系数、一次项系数、常数项分别是( )
| A. | 0、-2、-1 | B. | 1、2、-1 | C. | 1、-2、-1 | D. | 1、2、1 |
 如图,四点A、B、C、D,按照下列语句画出图形:
如图,四点A、B、C、D,按照下列语句画出图形: 如图,方格纸中每个小方格的边长为1,画一条长为$\sqrt{20}$的线段.
如图,方格纸中每个小方格的边长为1,画一条长为$\sqrt{20}$的线段. 已知:如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点M,N从点C同时出发,分别沿CA、CB方向匀速运动,速度都为1cm/s;同时,点P从点B出发,沿BA方向匀速运动,速度都为2cm/s,连接PM,PN,设时间为t(s)(0<t<2.5),解答下列问题:
已知:如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点M,N从点C同时出发,分别沿CA、CB方向匀速运动,速度都为1cm/s;同时,点P从点B出发,沿BA方向匀速运动,速度都为2cm/s,连接PM,PN,设时间为t(s)(0<t<2.5),解答下列问题: