Question

【题目】如图l，四边形中，，为的中点，为上一动点，连接并延长至点，使得，连接、、、.

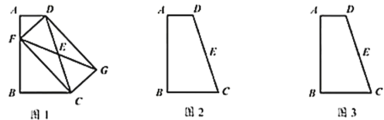
（1）四边形一定是___________（提醒你：填特殊四边形的名称）；

（2）如图2，若，，，是否存在这样的点，使得四边形为菱形，若存在，计算菱形的面积；若不存在，请说明理由.

（3）如图3，若，，（），是否存在这样的点，使得四边形为矩形，若存在，请求出的最大值；若不存在，请说明理由.

Answer 1

【答案】（1）见解析；（2）存在点，使得四边形为菱形，菱形的面积为45；（3）存在点，使得四边形为矩形，EF最大值为

【解析】

（1）根据对角线互相平分的四边形是平行四边形即可证明；（2）根据菱形定义可得DF=CF，根据勾股定理列方程求AF长，根据全等可证出∠DFC=90°，从而得四边形DFCG是正方形，根据面积公式求解；（3）根据矩形定义可得∠DFC=90°，根据相似得对应边成比例，列出m与AF长的关系，利用二次函数的最值问题确定m的最大值，再根据勾股定理求得DC长，即为EG长，从而确定EF的长.

解：（1）四边形DFCG一定是平行四边形，理由如下：

∵E为DC的中点，

∴DE=CE,

∵EG=FE,

∴四边形DFCG是平行四边形.

（2）存在点F，使得四边形为菱形，理由如下：

如图2, ∵四边形是平行四边形，

∴当DF=FC时，四边形是菱形,

∴AD2+AF2=BC2+BF2,

∴32+AF2=62+(9-AF)2

解得,AF=6，

∴AF=BC=6，AD=BF=3，∠A=∠B=90°,

∴△ADF≌CFB,

∴∠AFD=∠BCF,

∵∠BCF+∠BFC=90°,

∴∠AFD+∠BFC=90°,

∴∠DFC=90°,

∴四边形是正方形,

∴S四边形DFCG=DF2=AD2+AF2=32+62=45.

即当AF=6时，四边形是菱形，且面积为45.

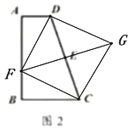
（3）存在点F，使得四边形为矩形，理由如下：

如图3, ∵四边形是平行四边形，

∴当∠DFC=90°时，四边形是矩形,

∴∠DFA+∠BFC=90°,

∵∠ADF+∠AFD=90°,

∴∠ADF=∠BFC,

∵∠A=∠B=90°,

∴△ADF∽△BFC,

∴

设AF=x，

∴，

∴ ，

∵m与x成二次函数关系，且a= ,

∴抛物线开口向下，m有最大值，

∴当x= 时，m的最大值为 .

作DM⊥BC，垂足为M，由勾股定理得，DC2=DM2+CM2

∴当m为最大值时，DC长最大为 ，

∵四边形是矩形

∴EG=DC,

∴EF的最大值为 .