题目内容
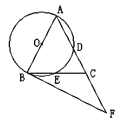
【题目】已知△ABC内接于⊙O，过点A作直线EF．
（1）如图①所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）： 或者 ．
（2）如图②所示，如果AB是不过圆心O的弦，且∠CAE=∠B，那么EF是⊙O的切线吗？试证明你的判断．
【答案】（1）①∠BAE=90°，②∠EAC=∠ABC
（2）EF是⊙O的切线
【解析】试题分析：（1）若EF是切线，则AB⊥EF，添加的条件只要能使AB⊥EF即可；
（2）作直径AM，连接CM，理由圆周角定理以及直径所对的圆周角是直角即可．
试题解析：（1）∠BAE＝90°；∠CAE＝∠B ；
EF是⊙O的切线．
作直径AM，连接CM，则∠ACM＝90°，∠M＝∠B，∴∠M＋∠CAM＝∠B＋∠CAM＝90°，∵∠CAE＝∠B，∴∠CAM＋∠CAE＝90°，∴AE⊥AM，∵AM为直径，∴EF是⊙O的切线．
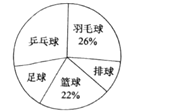
【题目】某中学为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1500名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称 | 人数 |
乒乓球 | 42 |
羽毛球 | a |
排球 | 15 |
篮球 | 33 |
足球 | b |
解答下列问题：
（1）这次抽样调查中的样本是________；
（2）统计表中，a=________，b=________；
（3）试估计上述1500名学生中最喜欢乒乓球运动的人数.
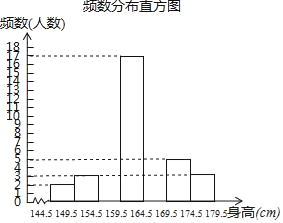
【题目】为了解同学们的身体发育情况，学校体卫办公室对七年级全体学生进行了身高测量（精确到1cm），并从中抽取了部分数据进行统计，请根据尚未完成的频数分布表和频数分布直方图解答下列问题：
频率分布表
分组 | 频数 | 百分比 |
144.5～149.5 | 2 | 4% |
149.5～154.5 | 3 | 6% |
154.5～159.5 | a | 16% |
159.5～164.5 | 17 | 34% |
164.5～169.5 | b | n% |
169.5～174.5 | 5 | 10% |
174.5～179.5 | 3 | 6% |
（1）求a、b、n的值；
（2）补全频数分布直方图；
（3）学校准备从七年级学生中选拔护旗手，要求身高不低于170cm，如果七年级有学生350人，护旗手的候选人大概有多少？
