题目内容
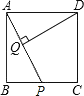
【题目】如图,![]() 在
在![]() 上,
上,![]() 经过圆心
经过圆心![]() 的线段
的线段![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() .
.
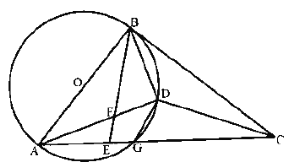
(1)如图1,当![]() 半径为
半径为![]() ,若
,若![]() ,求弦
,求弦![]() 的长;
的长;
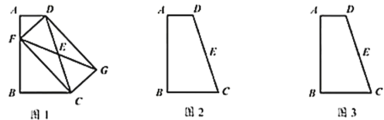
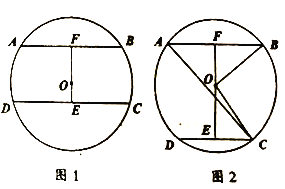
(2)如图2,当![]() 半径为
半径为![]() ,
,![]() ,若
,若![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)8 (2)![]()
【解析】
(1)连接![]() ,根据垂径定理求出
,根据垂径定理求出![]() 的长,因为
的长,因为![]() ,进而在
,进而在![]() 中根据勾股定理求出
中根据勾股定理求出![]() 长,所以求出
长,所以求出![]() 的长即可;
的长即可;
(2) 连接![]() ,过点D作
,过点D作![]() 于点M,根据勾股定理和垂径定理求出
于点M,根据勾股定理和垂径定理求出![]() ,可以证明
,可以证明![]() ,进而求出
,进而求出![]() 的长,根据所做的辅助线
的长,根据所做的辅助线![]() ,可得
,可得![]() 为等腰直角三角形,所以可以求出
为等腰直角三角形,所以可以求出![]() 的长,然后根据
的长,然后根据![]() ,进而求出
,进而求出![]() 的长;
的长;
解:(1) 连接![]() ,根据垂径定理求出
,根据垂径定理求出![]() 的长,
的长,
即:![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
由勾股定理得:
![]() ,
,
即:![]() ,
,
解得:![]() ,
,
![]() ;
;

(2)连接![]() ,过点D作
,过点D作![]() 于点M,如图所示:
于点M,如图所示:
![]() ,
,
![]() 在
在![]() 中根据勾股定理可得:
中根据勾股定理可得:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
而![]() ,
,
![]() ,
,
又![]() 在
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
把![]() 代入到
代入到![]() 中,
中,
解得:![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.