题目内容
【题目】阅读下面材料，完成（1）～（3）题．
数学课上，老师出示了这样一道题：
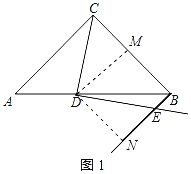
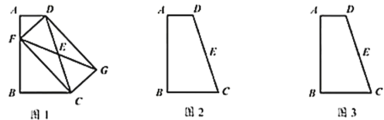
如图1，△ABC中，AC＝BC＝a，∠ACB＝90°，点D在AB上，且AD＝kAB（其中0＜k＜
），直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E，探究线段DC、DE的数量关系，并证明．
同学们经过思考后，交流了自己的想法：
小明：“通过观察和度量，发现DC与DE相等”；
小伟：“通过构造全等三角形，经过进一步推理，可以得到DC与DE相等”
小强：“通过进一步的推理计算，可以得到BE与BC的数量关系”
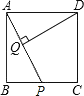
老师：“保留原题条件，连接CE交AB于点O．如果给出BO与DO的数量关系，那么可以求出COEO的值”
（1）在图1中将图补充完整，并证明DC＝DE；
（2）直接写出线段BE与BC的数量关系 （用含k的代数式表示）；
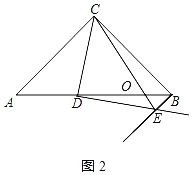
（3）在图2中将图补充完整，若BO＝
DO，求COEO的值（用含a的代数式表示）．
【答案】（1）证明见解析；（2）BE＝（1﹣2k）BC；（3）
【解析】
（1）作DM⊥BC于M，DN作BE于N，则∠DMC=∠DNE=90°，由等腰直角三角形的性质得出∠ABC=45°，AB=
BC=a，由旋转的性质得∠CDE=∠CBE=90°，则∠DBE=45°，∠MDN=90°，∠CDM=∠EDN，∠ABC=∠ABE，由角平分线的性质得出DM=DN，由ASA证得△CDM≌△EDN（ASA），即可得出结论；
（2）由（1）得△CDM≌△EDN，则CM=EN，易证四边形BMDN是矩形，△BDM是等腰直角三角形，证明四边形BMDN是正方形，得出BM=BN，推出BC+BE=BM+CM+BM-CM=2BM=BD，BD=AB-AD=（1-k）AB=（1-k）BC，则BC+BE=BD=2（1-k）BC，即可得出结果；
（3）由∠CDE+∠CBE=90°+90°=180°，得出B、C、D、E四点共圆，得出COEO=DOBO，即可得出结果．
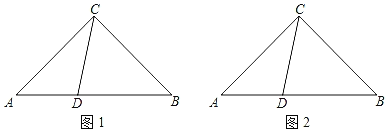
解：（1）将图补充完整，如图1所示：
作DM⊥BC于M，DN作BE于N，
则∠DMC＝∠DNE＝90°，
∵AC＝BC＝a，∠ACB＝90°，
∴∠ABC＝45°，AB＝BC＝
，
由旋转的性质得：∠CDE＝∠CBE＝90°，
∴∠DBE＝90°﹣45°＝45°，∠MDN＝90°，
∴∠CDM＝∠EDN，∠ABC＝∠ABE，
∵DM⊥BC于M，DN作BE于N，
∴DM＝DN，
在△CDM和△EDN中，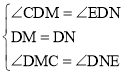
，
∴△CDM≌△EDN（ASA），
∴DC＝DE；
（2）BE＝（1﹣2k）BC，理由如下：
由（1）得：△CDM≌△EDN，
∴CM＝EN，
∵∠CBE＝90°，DM⊥BC，DN⊥BE，
∴四边形BMDN是矩形，
∵∠ABC＝45°，
∴△BDM是等腰直角三角形，
∴DM＝BM，BM＝
BD，
∴四边形BMDN是正方形，
∴BM＝BN，
∵BC＝BM+CM，
∴BC+BE＝BM+CM+BM﹣CM＝2BM＝
BD，
∵AD＝kAB，
∴BD＝AB﹣AD＝（1﹣k）AB＝（1﹣k）BC，
∴BC+BE＝BD＝2（1﹣k）BC，
整理得：BE＝（1﹣2k）BC；
故答案为：BE＝（1﹣2k）BC；
（3）将图补充完整，如图2所示：
∵∠CDE+∠CBE＝90°+90°＝180°，
∴B、C、D、E四点共圆，
∴COEO＝DOBO，
∵BO＝
DO，
∴COEO＝DOBO＝DO2＝×（
BD）2＝×（）2×[（1﹣k）a]2＝
．
