题目内容
阅读下列材料:
问题:如图1,在□ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线
EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理使
问题得到解决.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

图1 图2
解:(1)证明:如图,作∠GAH=∠EAB交GE于点H.
∴∠GAB=∠HAE. ………………………………………………………1分
∵∠EAB=∠EGB,∠APE=∠BPG,
∴∠ABG=∠AEH. …………………………………………………………2分
 ∵又AB=AE,
∵又AB=AE,
∴△ABG≌△AEH. …………3分
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG. ……………………………………………………………4分
(2)线段EG、AG、BG之间的数量关系是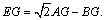 …………5分
…………5分
理由如下:
 如图,作∠GAH=∠EAB交GE的延长线于点H.
如图,作∠GAH=∠EAB交GE的延长线于点H.
∴∠GAB=∠HAE.
∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH =180°.
∴∠ABG=∠AEH.
∵又AB=AE,
∴△ABG≌△AEH. ………………6分
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴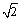 AG=HG.
AG=HG.
∴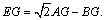 …………………………………………………………7分
…………………………………………………………7分

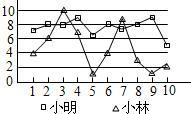
甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
| 选 手 | 甲 | 乙 | 丙 | 丁 |
| 平均数(环) | 9.2 | 9.2 |
| 9.2 |
| 方差(环2) | 0.035 | 0.015 | 0.025 | 0.027 |
则这四人中成绩发挥最稳定的是
A.甲 B.乙 C.丙 D.丁


 品件数的2倍件数还少10件,购买三等奖奖品所花钱数不超过二等奖所花钱数的1.5倍,且三等奖奖品数不能少于前两种奖品数之和.其中各种奖品的单价如下表所示,如果计划一等奖奖品买x件,买50件奖品的总费用是w元.
品件数的2倍件数还少10件,购买三等奖奖品所花钱数不超过二等奖所花钱数的1.5倍,且三等奖奖品数不能少于前两种奖品数之和.其中各种奖品的单价如下表所示,如果计划一等奖奖品买x件,买50件奖品的总费用是w元.

 9.2
9.2 = ,
= ,
