题目内容
14. 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次联结这六条线段外端点可以得到一个新的正六边形,那么AB:A′B′的值是( )
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次联结这六条线段外端点可以得到一个新的正六边形,那么AB:A′B′的值是( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | $\sqrt{2}:\sqrt{3}$ | D. | 1:$\sqrt{3}$ |
分析 根据六边形ABCDEF是正六边形,得到∠A′CB′=60°,设AB=BC=a,则A′C=2a,然后求得A′B′=A′C•sin60°=$\sqrt{3}$a,从而求得两条边的比.
解答 解:∵六边形ABCDEF是正六边形,
∴∠A′CB′=60°,
设AB=BC=a,则A′C=2a,
∴A′B′=A′C•sin60°=$\sqrt{3}$a,
∴AB:A′B′=a:$\sqrt{3}$a=1:$\sqrt{3}$,
故选D.
点评 本题考查的是正多边形和圆,解答此题的关键是熟知正多边形内角的性质及直角三角形的判定定理.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
6.下列四个数中,在-2和-1之间的是( )
| A. | -$\frac{1}{10}$ | B. | -$\frac{9}{10}$ | C. | -$\frac{11}{10}$ | D. | -$\frac{23}{10}$ |
5.下列说法中,正确的是( )
| A. | 对顶角相等 | B. | 补角相等 | C. | 锐角相等 | D. | 同位角相等 |
2.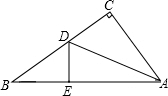 如图,有一个直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是( )cm.
如图,有一个直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是( )cm.
 如图,有一个直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是( )cm.
如图,有一个直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是( )cm.| A. | 3 | B. | 4 | C. | $3\frac{1}{3}$ | D. | $4\frac{2}{3}$ |
4.列方程(组)解应用题:
某超市的部分商品账目记录显示内容如下:
求第三天卖出牙膏多少盒.
某超市的部分商品账目记录显示内容如下:
| 商品 时间 | 第一天 | 第二天 | 第三天 |
| 牙膏(盒) | 7 | 14 | ? |
| 牙刷(支) | 13 | 15 | 12 |
| 营业额(元) | 121 | 187 | 124 |
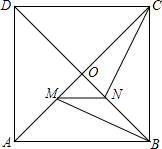 如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.
如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.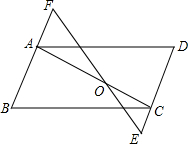 如图,已知AB=CD,AD=BC,O为AC上任意一点,过O点作直线分别交BA,DC的延长线于点F,E,求证:∠E=∠F.
如图,已知AB=CD,AD=BC,O为AC上任意一点,过O点作直线分别交BA,DC的延长线于点F,E,求证:∠E=∠F.