Question

杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体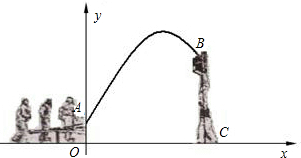（看成一点）的路线是抛物线y=-

3

5

x²+3x+1的一部分，如图：
（1）求演员弹跳离地面的最大高度；
（2）已知人梯高BC=3.8m，在一次表演中，人梯到起跳点A的水平距离是4m，问这次表演是否成功？若能成功，请通过计算说明理由；若不能成功，应如何调整人梯的高度？

Answer 1

分析：（1）将二次函数化简为y=-

3

5

（x-

5

2

）²+

19

4

，即可解出y_最大的值．
（2）当x=4时代入二次函数可得点B的坐标在抛物线上．

解答：解：（1）将二次函数y=-

3

5

x²+3x+1化成y=-

3

5

（x -

5

2

）² +

19

4

，
当x=

5

2

时，y有最大值，y_最大值=

19

4

，（5分）
因此，演员弹跳离地面的最大高度是4.75米．

（2）不能成功表演．理由是：把y=3.8代入y=-

3

5

x²+3x+1得：x=

15± 57

6

，
即x的取值范围是0≤x≤

15+ 57

6

，
当x=4时，y=-

3

5

×4²+3×4+1=3.4．
∵3.4＜3.8，
因此，不能表演成功，可以将人梯高调整为3.4米．

点评：本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题，遇到这样的应用题不要害怕，认真读懂题意是关键．