题目内容
18.某瓜果基地市场部为指导该基地某种蔬菜的生产销售,在对历年市场行情和生产情况进行调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图(注:两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图象是直线,图乙的图象是抛物线)
请你根据图象提供的信息,解答下列问题:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由.
(3)已知市场部销售该种蔬菜,4,5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万千克,求4,5两个月销量各多少万千克?
分析 (1)由图知3月份的售价是5元,成本是4元,所以收益是1元;
(2)需分别求出x月份的成本和售价,因此须求两图象对应的解析式,根据收益的表达式求最值.
(3)假设出4月份的销量为x万公斤,则5月份的销量为(x+2)万公斤,利用两月的每千克利润即可得出答案.
解答 解:(1)在3月份,每千克售价为5元,在3月份,每千克成本为4元
∴在3月份出售这种蔬菜,每千克收益是1元;
(2)设x月份出售时,每千克售价为y1元,每千克成本为y2元
根据图(1)设y1=kx+b
∴$\left\{\begin{array}{l}{3k+b=5}\\{6k+b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=7}\end{array}\right.$,
∴y1=-$\frac{2}{3}$x+7,
根据图(2)设y2=a(x-6)2+1
∴4=a(3-6)2+1
∴a=$\frac{1}{3}$
∴y2=$\frac{1}{3}$(x-6)2+1
$\frac{1}{3}$(x-6)2+1
∵y=y1-y2
∴y=-$\frac{2}{3}$x+7-[$\frac{1}{3}$(x-6)2+1],
y=-$\frac{1}{3}$x2+$\frac{10}{3}$x-6=-$\frac{1}{3}$(x-5)2+$\frac{7}{3}$.
∴当x=5时,y有最大值即当5月份出售时,每千克收益最大.
(3)假设出4月份的销量为x,则5月份的销量为(x+2)kg,
∵4,5月每千克售价分别为:y1=-$\frac{2}{3}$x+7=-$\frac{2}{3}$×4+7=$\frac{13}{3}$,y1=-$\frac{2}{3}$×5+7=$\frac{11}{3}$,
4,5月每千克成本分别为:y2=$\frac{1}{3}$(x-6)2+1=$\frac{1}{3}$(4-6)2+1=$\frac{7}{3}$元,
∴y2=$\frac{1}{3}$(x-6)2+1=$\frac{1}{3}$(5-6)2+1=$\frac{4}{3}$元,
∴4,5月的每千克的利润为:$\frac{13}{3}$-$\frac{7}{3}$=2元,$\frac{11}{3}$-$\frac{4}{3}$=$\frac{7}{3}$元,
∴2x+(x+2)×$\frac{7}{3}$=48,
解得:x=10万公斤,
∴x+2=12万公斤,
∴4、5两个月销量各10万公斤、12万公斤.
点评 此题主要考查了函数的综合应用,结合函数图象得出各点的坐标,再利用待定系数法求出函数解析式是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 5 | C. | 12 | D. | 13 |
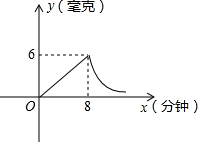 为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题:
为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题: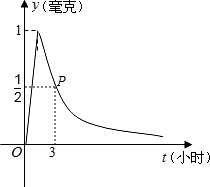 为了预防流感,某图书馆用药熏消毒法对其阅览厅进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t成反比例(如图所示).根据图中提供的信息,解答下列问题:
为了预防流感,某图书馆用药熏消毒法对其阅览厅进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t成反比例(如图所示).根据图中提供的信息,解答下列问题: 三个微生物(分别标号为1,2,3)第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物.那么标号为100的微生物会出现在( )
三个微生物(分别标号为1,2,3)第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物.那么标号为100的微生物会出现在( ) 如图,已知AB∥CD,则图中∠1,∠2,∠3的关系是∠1=∠2+∠3.
如图,已知AB∥CD,则图中∠1,∠2,∠3的关系是∠1=∠2+∠3.