Question

9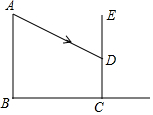．如图，一位同学想利用建筑物的影子测量建筑物AB的高度，他在某一时刻测得直立的标杆高为1m时，影长为1.2m，他立即又测量建筑物的影子，因建筑物AB靠近另一个建筑物CE，所以AB的影子没有完全落在地上，一部分影子落在墙上，他测得地上部分的影子长BC为7.2m，又测得墙上部分的影子高CD为1.2m，请你帮他计算建筑物AB的高度．

Answer 1

分析 过D点作DH⊥AB于H，如图．则DH=BC=7.2m，BH=CD=1.2m，根据“在同一时刻物高与影长的比相等“得到$\frac{AH}{7.2}$=$\frac{1}{1.2}$，则可计算出AH，然后计算AH+BH即可．

解答 解：过D点作DH⊥AB于H，如图，则DH=BC=7.2m，BH=CD=1.2m，
∵在某一时刻测得直立的标杆高为1m时，影长为1.2m，
∴$\frac{AH}{HD}$=$\frac{1}{1.2}$，即$\frac{AH}{7.2}$=$\frac{1}{1.2}$，
∴AH=6，
∴AB=AH+BH=6+1.2=7.2（m）
答：建筑物AB的高度为7.2m．

点评 本题考查了相似三角形的应用：通常利用相似三角形的性质即相似三角形的对应边成比例和“在同一时刻物高与影长的比相等”的原理解决．