题目内容
 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB= ,AB=2,求
,AB=2,求 的值.
的值.
解:根据题意得:点A的坐标为(-n,0),点Q的坐标为(0,n),点B的坐标为( ,0),
,0),
∵点P是PA与PB的交点,
∴ ,
,
解得: ,
,
∴点P的坐标为:( ,
, ),
),
∵AB=2,
∴OA+OB=n+ =
= =2,
=2,
∴m+2n=4,
∵S四边形PQOB= ,
,
∴S△PAB-S△AOQ= ×2×
×2× -
- n×n=
n×n= -
- n2=
n2= ,
,
解得:n=1,
∴m=2,
∴ =
= =
= .
.
分析:由题意可求得点A,B,Q,P的坐标,又由S四边形PQOB= ,AB=2,即可求得m与n的值,代入即可求得
,AB=2,即可求得m与n的值,代入即可求得 的值.
的值.
点评:此题考查了一次函数上点的坐标特征以及四边形的面积问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.
 ,0),
,0),∵点P是PA与PB的交点,
∴
 ,
,解得:
 ,
,∴点P的坐标为:(
 ,
, ),
),∵AB=2,
∴OA+OB=n+
 =
= =2,
=2,∴m+2n=4,
∵S四边形PQOB=
 ,
,∴S△PAB-S△AOQ=
 ×2×
×2× -
- n×n=
n×n= -
- n2=
n2= ,
,解得:n=1,
∴m=2,
∴
 =
= =
= .
.分析:由题意可求得点A,B,Q,P的坐标,又由S四边形PQOB=
 ,AB=2,即可求得m与n的值,代入即可求得
,AB=2,即可求得m与n的值,代入即可求得 的值.
的值.点评:此题考查了一次函数上点的坐标特征以及四边形的面积问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象. 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB= 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB= 的图象,直线PB是一次函数
的图象,直线PB是一次函数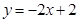 的图象.
的图象.
 ,AB=2,则
,AB=2,则 =( )
=( )



