Question

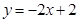如图，直线PA是一次函数的图象，直线PB是一次函数的图象．

（1）求A、B、P三点的坐标；（2）求四边形PQOB的面积；

 

Answer 1

【答案】

(1)A（-1，0），B（1，0），；（2）

【解析】

试题分析：本题考查了一次函数综合题，难度一般，关键是掌握把四边形的面积分成两个三角形面积的差进行求解．（1）令一次函数y=x+1与一次函数y=-2x+2的y=0可分别求出A，B的坐标，再由 y＝x+1和 y＝−2x+2 构建二元一次方程组，可求出点P的坐标；

（2）根据四边形PQOB的面积=S△BOM-S△QPM即可求解．

试题解析：

解：（1）∵一次函数y=x+1的图象与x轴交于点A，

∴A（-1，0），

∵一次函数y=-2x+2的图象与x轴交于点B，

∴B（1，0），

∵一次函数y=x+1的图象与一次函数y=-2x+2的图象交与点P

∴解得：

∴点P的坐标是：

（2）∵直线PA与y轴交于点Q，则Q（0，1），设直线PB与y轴交于点M，则M（0，2），

∴.

考点：一次函数综合题．