题目内容
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB= ,AB=2,则
,AB=2,则 =( )
=( )
A.

B.

C.

D.

【答案】分析:观察图形可以求出两直线的交点坐标,两直线与x轴的交点坐标,利用S四边形PQOB= ,AB=2列出两个关于m,n的方程,解出m.n即可.
,AB=2列出两个关于m,n的方程,解出m.n即可.
解答:解:两直线相交得:P(
,
),A(-n,0),B( ,0),Q(0,n),
,0),Q(0,n),
∵AB=n+
=2,即m+2n=4,①
又∴S四边形PQOB=S△PAB-S△AOQ=
×2×
-
n2=
,
∴2(m+2n)-3n2=5,②
由①②得n=1,m=2,
∴ =
= ,
,
故选C.
点评:本题考查了一次函数的综合应用;认真读题,在理解题意的基础上列出方程式正确解答本题的关键.
 ,AB=2列出两个关于m,n的方程,解出m.n即可.
,AB=2列出两个关于m,n的方程,解出m.n即可.解答:解:两直线相交得:P(
| m-n |
| 3 |
| m+2n |
| 3 |
 ,0),Q(0,n),
,0),Q(0,n),∵AB=n+
| m |
| 2 |
又∴S四边形PQOB=S△PAB-S△AOQ=
| 1 |
| 2 |
| m+2n |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
∴2(m+2n)-3n2=5,②
由①②得n=1,m=2,
∴
 =
= ,
,故选C.
点评:本题考查了一次函数的综合应用;认真读题,在理解题意的基础上列出方程式正确解答本题的关键.

练习册系列答案
相关题目
 如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象. 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB= 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB= 的图象,直线PB是一次函数
的图象,直线PB是一次函数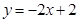 的图象.
的图象.