��Ŀ����
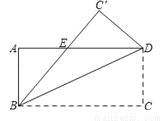
��ͼ����������ABCD�ضԽ���BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E��
��1�����жϡ�BDE����״����˵�����ɣ�
��2����AB=4��AD=8�����BDE�������
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����������ABCD�ضԽ���BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E��
��1�����жϡ�BDE����״����˵�����ɣ�
��2����AB=4��AD=8�����BDE�������
