题目内容
15.若$\sqrt{{x}^{2}(x+1)}$=-x$\sqrt{x+1}$成立,则x的取值范围为-1≤x≤0.分析 根据题意得出关于x的不等式组,求出x的取值范围即可.
解答 解:∵$\sqrt{{x}^{2}(x+1)}$=-x$\sqrt{x+1}$成立,
∴$\left\{\begin{array}{l}x≤0\\ x+1≥0\end{array}\right.$,解得-1≤x≤0.
故答案为:-1≤x≤0.
点评 本题考查的是二次根式的性质与化简,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
相关题目
6.若y=ax2+bx+c,则由表中信息可知:y与x之间的函数关系式是( )
| x | -1 | 0 | 1 |
| ax2 | |||
| ax2+bx+c | 8 | 3 | 0 |
| A. | y=x2-4x+3 | B. | y=x2-2x+4 | C. | y=x2-3x+3 | D. | y=x2-4x+8 |
10.下列各式中,运算正确的是( )
| A. | (-5.8)-(-5.8)=-11.6 | B. | [(-5)2+4×(-5)]×(-3)2=-45 | ||
| C. | -23×(-3)2=-72 | D. | $-{4^2}÷\frac{1}{4}×\frac{1}{4}=-1$ |
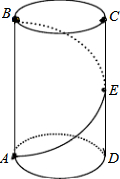 如图,一只螳螂在树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是就绕到虫子后面吃掉它,已知树干的半径为10cm,A,B两点的距离为45cm,求螳螂爬行的最短距离(π取3).
如图,一只螳螂在树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是就绕到虫子后面吃掉它,已知树干的半径为10cm,A,B两点的距离为45cm,求螳螂爬行的最短距离(π取3).