题目内容
 在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.
在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.(1)若∠BAC=90°,求证:四边形ADCH是菱形;
(2)若DE=3,BC=8,求△FCD的面积.
考点:菱形的判定与性质
专题:
分析:(1)首先判定四边形ADCH是平行四边形,然后由直角三角形斜边上的中线等于斜边的一边判定AD=CD,则易推知结论;
(2)首先过A作AG⊥CD,垂足为G,易得△BDE∽△BGA,可求得AG的长,继而求得△ABC的面积,然后由相似三角形面积比等于相似比的平方,求得△FCD的面积.
(2)首先过A作AG⊥CD,垂足为G,易得△BDE∽△BGA,可求得AG的长,继而求得△ABC的面积,然后由相似三角形面积比等于相似比的平方,求得△FCD的面积.
解答: (1)证明:如图,∵CG∥AD,AH∥CD,
(1)证明:如图,∵CG∥AD,AH∥CD,
∴四边形ADCH是平行四边形.
∵∠BAC=90°,D是BC的中点,
∴AD=CD,
∴四边形ADCH是菱形;
(2)过A作AM⊥CD,垂足为M.
∵AD=AC,
∴DG=CM,
∴BD:BM=2:3,
∵ED⊥BC,
∴ED∥AG,
∴△BDE∽△BMA,
∴ED:AM=BD:BM=2:3,
∵DE=3,
∴AM=
,
∵△ABC∽△FCD,BC=2CD,
∴
=(
)2=
.
∵S△ABC=
×BC×AM=
×8×
=18,
∴S△FCD=
S△ABC=
.
 (1)证明:如图,∵CG∥AD,AH∥CD,
(1)证明:如图,∵CG∥AD,AH∥CD,∴四边形ADCH是平行四边形.
∵∠BAC=90°,D是BC的中点,
∴AD=CD,
∴四边形ADCH是菱形;
(2)过A作AM⊥CD,垂足为M.
∵AD=AC,
∴DG=CM,
∴BD:BM=2:3,
∵ED⊥BC,
∴ED∥AG,
∴△BDE∽△BMA,
∴ED:AM=BD:BM=2:3,
∵DE=3,
∴AM=
| 9 |
| 2 |
∵△ABC∽△FCD,BC=2CD,
∴
| S△FCD |
| S△ABC |
| CD |
| BC |
| 1 |
| 4 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴S△FCD=
| 1 |
| 4 |
| 9 |
| 2 |
点评:此题考查了菱形的判定与性质、相似三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,正方形网格中每个小正方形的边长为1.
如图,正方形网格中每个小正方形的边长为1. 如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于
如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于 如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.
如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.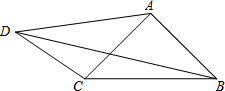 如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为
如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为