题目内容
如图,在△ABC中,∠BAC=90°,AB=AC,AE是经过A的一条直线,BD⊥AE与D,CE⊥AE与E,
(1)若D,E在BC的同侧,探索BD,CE,DE的关系,并加以证明
(2)若D,E分布在BC两侧,问题(1)成立吗?若不成立,则关系又是如何呢?并加以证明.
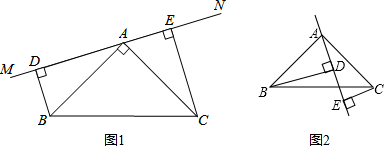
(1)若D,E在BC的同侧,探索BD,CE,DE的关系,并加以证明
(2)若D,E分布在BC两侧,问题(1)成立吗?若不成立,则关系又是如何呢?并加以证明.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证∠EAC=∠ABD,即可求证△ABD≌△CAE,根据全等三角形相等的性质即可解题.
(2)根据全等三角形的判定得到可得△ABD≌△CAE,利用全等的性质得BD=AE,AD=CE,由AE=AD+DE,即可得到BD=DE+CE.
(2)根据全等三角形的判定得到可得△ABD≌△CAE,利用全等的性质得BD=AE,AD=CE,由AE=AD+DE,即可得到BD=DE+CE.
解答:
 解:(1)DE=BD+CE.理由如下:
解:(1)DE=BD+CE.理由如下:
如图1,∵∠DAB+∠EAC=90°,∠DAB+∠ABD=90°,
∴∠EAC=∠ABD,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=AD,
∵DE=AD+AE,
∴DE=BD+CE;
(2)(1)中的关系不成立,应该是BD=DE+CE.理由如下:
如图2,∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°
∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
∴∠ABD=∠EAC,
在△ABD和△ACE中
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE.
 解:(1)DE=BD+CE.理由如下:
解:(1)DE=BD+CE.理由如下:如图1,∵∠DAB+∠EAC=90°,∠DAB+∠ABD=90°,
∴∠EAC=∠ABD,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=AD,
∵DE=AD+AE,
∴DE=BD+CE;
(2)(1)中的关系不成立,应该是BD=DE+CE.理由如下:
如图2,∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°
∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
∴∠ABD=∠EAC,
在△ABD和△ACE中
|
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABD≌△CAE是解题的关键.

练习册系列答案
相关题目
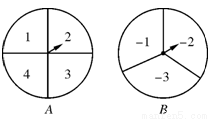
若方程x2-(m2-4)x+m=0的两个实根互为相反数,则m的值是( )
| A、0 | B、2 | C、-2 | D、-2或2 |
 在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是E、F.
在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是E、F.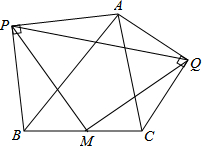 如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.
如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.