题目内容
5.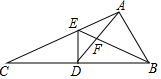 如图,在△ABC中,D是BC边的中点,DE⊥BC,交AC于点E,AD交BE于点F,若已知AD=AB.
如图,在△ABC中,D是BC边的中点,DE⊥BC,交AC于点E,AD交BE于点F,若已知AD=AB.(1)求证:∠CAD=∠ABE;
(2)求证:AF=DF.
分析 (1)根据线段垂直平分线的性质得到CE=BE,由等腰三角形的性质得到∠C=∠CBE,∠ADB=∠ABD,于是得到结论;
(2)过F点作BC的平行线交AC于M、交AB于N,根据平行线的性质得到∠C=∠AMF,∠BFN=∠DBF,等量代换得到∠AMF=∠BFN,根据相似三角形的性质得到$\frac{MF}{CD}=\frac{AF}{AD}=\frac{FN}{BD}$,推出FM=FN,根据全等三角形的性质得到AF=BN,根据线段的和差即可得到结论.
解答 解:(1)∵D是BC边的中点,DE⊥BC,
∴CE=BE,
∴∠C=∠CBE,
∵AD=AB,
∴∠ADB=∠ABD,
∵∠ADB=∠CAD+∠C,∠ABC=∠ABE+∠DBE,
∴∠CAD=∠ABE;
(2)过F点作BC的平行线交AC于M、交AB于N,
∵MN∥BC,
∴∠C=∠AMF,∠BFN=∠DBF,
∵∠C=∠CBE,
∴∠AMF=∠BFN,
∵MN∥BC,
∴△AMF∽△ACD,△AFN∽△ADB,
∴$\frac{MF}{CD}=\frac{AF}{AD}=\frac{FN}{BD}$,
∵CD=BD,
∴FM=FN,
在△AFM与△BFN中,$\left\{\begin{array}{l}{∠AMF=∠BFN}\\{∠MAF=∠NBF}\\{MF=FN}\end{array}\right.$,
∴△AFM≌△BFN
∴AF=BN,
∵△ABD是等腰三角形,
∴BN=DF,
∴AF=DF.
点评 本题考查了线段的垂直平分线的性质,全等三角形的判断和性质,相似三角形的判定和性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 按要求作图:已知如图平面直角坐标系中,A点在第二象限到两坐标轴的距离都为4,C点位于第一象限且到x轴的距离为3,到y轴的距离为1,过A点作AB⊥x轴于B点,解答下列各题:
按要求作图:已知如图平面直角坐标系中,A点在第二象限到两坐标轴的距离都为4,C点位于第一象限且到x轴的距离为3,到y轴的距离为1,过A点作AB⊥x轴于B点,解答下列各题: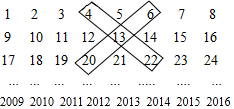
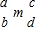 表示类似“X”形框中的5个数,试用等式写出a、b、c、d、m这五个字母之间的关系a+b+c+d=4m(写出一个即可).
表示类似“X”形框中的5个数,试用等式写出a、b、c、d、m这五个字母之间的关系a+b+c+d=4m(写出一个即可).