Question

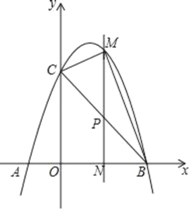
【题目】如图，已知抛物线y＝ax2+bx+3与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，连接BC．

（1）求抛物线的解析式；

（2）若点P为线段BC上的一动点（不与B、C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求点P的坐标；

（3）在（2）的条件下，当△BCM的面积最大时，点D是抛物线的对称轴上的动点，在抛物线上是否存在点E，使得以A、P、D、E为顶点的四边形为平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝﹣x2+2x+3．（2）当t＝时，△BCM的面积最大．此时，点P的坐标为（，）．（3）存在点E使得以A、P、D、E为顶点的四边形为平行四边形，点E的坐标是或（）或（）．

【解析】

（1）由y＝ax2+bx+3经过点A、B、C，A（﹣1，0）、B（3，0），利用待定系数法即可求得此抛物线的解析式；

（2）设直线BC的解析式为y＝kx+b，由待定系数法即可求得直线BC的解析式，再设P（t，﹣t+3），即可得M点坐标为（t，﹣t2+2t+3），即可求得PM的长，由S△BCM＝S△PMC+S△PMB，即可得S△BMC＝﹣（t﹣）2+，利用二次函数的性质，即可求得当△BDC的面积最大时，求点P的坐标；

(3)由于此题没有说明四边形的顶点顺序故需分类讨论：①当四边形APDE为平行四边形时，利用xA﹣xP＝xE﹣xD即可求出xE的值，代入二次函数解析式即可；②当四边形APED为平行四边形时，同理；③当四边形ADPE为平行四边形时，此时xA+xP＝xD+xE即可求出xE的值，代入二次函数解析式即可.

解：（1）依题意得：，

解得：，

抛物线的解析式为y＝﹣x2+2x+3．

（2）设直线BC的解析式为y＝kx+b，则，

解得：，直线BC的解析式为y＝﹣x+3，

设点P坐标为（t，﹣t+3），则M点坐标为（t，﹣t2+2t+3），

∴PM＝﹣t2+2t+3+t﹣3＝﹣t2+3t，

∴S△BCM＝S△PMC+S△PMB＝＝，

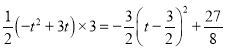∴当t＝时，△BCM的面积最大．此时，点P的坐标为（，）．

（3））∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，

∴对称轴为直线x＝1，

当四边形APDE为平行四边形时，

AP∥ED，AP＝ED，

∵A（﹣1，0），P（），

∴xA﹣xP＝xE﹣xD＝﹣1﹣，

∵xD＝1，

∴xE＝﹣，

∴E（，）；

当四边形APED为平行四边形时，

AP∥DE，AP＝DE，

∴xA﹣xP＝xD﹣xE＝﹣1﹣，

∵xD＝1，

∴xE＝，

∴E（，﹣）；

当四边形ADPE为平行四边形时，

AE∥DP，AE＝DP，

∴xA+xP＝xD+xE＝﹣1+，

∵xD＝1，

∴xE＝﹣，

∴E（﹣，）；

存在点E使得以A、P、D、E为顶点的四边形为平行四边形，点E的坐标是（，）或（，﹣）或（﹣，）．