题目内容
17.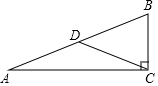 如图,已知△ABC中,∠ACB=Rt∠,∠A=30°,BC=6,D为AB的中点,则CD的长是( )
如图,已知△ABC中,∠ACB=Rt∠,∠A=30°,BC=6,D为AB的中点,则CD的长是( )| A. | 5 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
分析 先根据含30°的直角三角形的性质得出AB=12,再根据直角三角形斜边上的中线等于斜边的一半可得CD=$\frac{1}{2}$AB.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,
∴AB=12,
∵∠ACB=90°,D为AB的中点,
∴CD=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6.
故选:C.
点评 本题考查了含30度角的直角三角形,直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
9.到三角形三个顶点的距离都相等的点是这个三角形的( )
| A. | 三条高的交点 | B. | 三条边的垂直平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条角平分线的交点 |
6.在(-1)2015,(-1)2016,-22,(-3)2四个数中,最大数与最小数的积等于( )
| A. | -4 | B. | -9 | C. | -36 | D. | -1 |
7.有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为m千克,再从中截出5米长的钢筋,称出它的质量为n千克,那么这捆钢筋的总长度为( )
| A. | $\frac{m}{n}$米 | B. | $\frac{5m}{n}$米 | C. | $\frac{mn}{5}$米 | D. | ($\frac{5m}{n}$-5)米 |
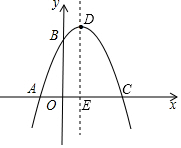 已知抛物线C1经过A(-1,0),B(0,3),C(3,0)三点,其顶点为点D,对称轴与x轴交于点E.
已知抛物线C1经过A(-1,0),B(0,3),C(3,0)三点,其顶点为点D,对称轴与x轴交于点E.