题目内容
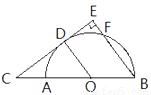
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

 名校课堂系列答案
名校课堂系列答案