题目内容
2.已知AB为⊙O的弦,OC⊥AB,垂足为C,若OA=10,AB=16,则OC的长为( )| A. | 12 | B. | 10 | C. | 6 | D. | 8 |
分析 先求出半弦AC的长,再利用勾股定理即可求出.
解答  解:在Rt△AOC中,
解:在Rt△AOC中,
∵OA=10cm,根据OC⊥AB,则AC=$\frac{1}{2}$AB=8,
∴OC=$\sqrt{1{0}^{2}-{8}^{2}}$=6.
故选C.
点评 此题考查了垂径定理、勾股定理;熟练掌握垂径定理,由勾股定理求出AC是解本题的关键.

练习册系列答案
相关题目
10.实数-π,-3.14,0,$\sqrt{2}$四个数中,最小的是( )
| A. | -3.14 | B. | -π | C. | $\sqrt{2}$ | D. | 0 |
17.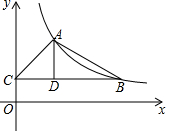 如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )
如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )
 如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )
如图,在△ABC中,BC∥x轴,AD⊥BC,A,B两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,若S△ACD=6,S△ABD=9,则k为( )| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
7.中国科学家屠呦呦获得了诺贝尔生理学或医学奖,她研发的抗疟新药每年能为近120万婴幼儿免除疟疾的危害.其中120万用科学记数法表示为( )
| A. | 12×103 | B. | 1.2×104 | C. | 1.2×106 | D. | 1.2×108 |
14.在一个不透明的袋子中装有三个小球,它们除分别标有的号码2,3,6不同外,其他完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则第二次摸出球的号码比第一次摸出球的号码大的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
11. 如图,四边形ABCD内接于⊙O,若它的一个外角∠BCE=65°,则∠BOD的大小为( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠BCE=65°,则∠BOD的大小为( )
 如图,四边形ABCD内接于⊙O,若它的一个外角∠BCE=65°,则∠BOD的大小为( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠BCE=65°,则∠BOD的大小为( )| A. | 65° | B. | 115° | C. | 130° | D. | 135° |
12.一个多边形的内角和是720°,这个多边形是( )
| A. | 六边形 | B. | 五边形 | C. | 四边形 | D. | 三角形 |
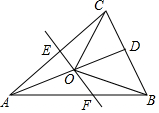 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是( )