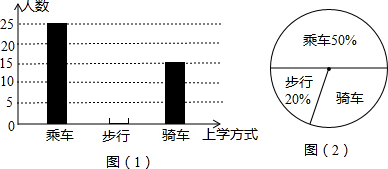
题目内容
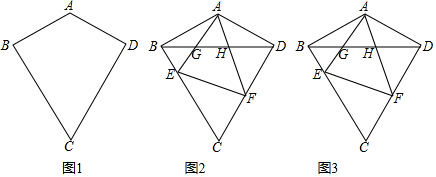
5.在四边形ABCD中,AB=AD,BC=CD.(1)如图1,请连接AC,BD,求证:AC垂直平分BD;
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出$\frac{GH}{BD}$的值.
分析 (1)如图1中,连接BD、AC.只要证明点A、点B在线段BD的垂直平分线上即可;
(2)如图2中,将△ABE绕点A逆时针旋转120得到△ADM.连接AC交BD于O.首先证明△FAE≌△FAM,再证明∠AGO=∠ADF,即可解决问题;
(3)如图3中,连接AC交BD于O,作HM⊥AD于M.由(2)可知∠AFD=∠AFE=∠AGO=45°,由∠ADF=90°,可得AD=DF,设HM=AM=a,则DH=2a,DM=$\sqrt{3}$a,想办法求出GH、BD(用a表示),即可解决问题;
解答 (1)证明:如图1中,连接BD、AC.
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴AC是线段BD的垂直平分线,
即AC垂直平分线段BD.
(2)如图2中,将△ABE绕点A逆时针旋转120得到△ADM.连接AC交BD于O.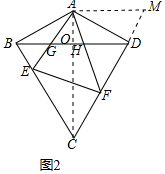
∵B、D关于AC对称,
∴∠ABC=∠ADC=90°,
∵∠BCD=60°,
∴∠BAD=120°,
∵∠EAF=60°,
∴∠BAE+∠DAF=∠DAF+∠DAM=60°,
∴∠FAE=∠FAM,
∵∠ADM=∠ABE=90°=∠ADF,
∴F、D、M共线,
∵FA=FA,AE=AM,
∴△FAE≌△FAM,
∴∠AFE=∠AFM,
∵∠CAD=∠CAB=60°=∠EAF,
∴∠GAO=∠DAF,
∵∠AGO+∠GAO=90°,∠AFD+∠FAD=90°,
∴∠AGO=∠ADF,
∴∠AGH=∠AFE,∵∠GAH=∠FAE,
∴△AGH∽△AFE.
(3)解:如图3中,连接AC交BD于O,作HM⊥AD于M.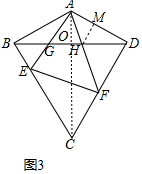
∵EF⊥CD,
∴∠EFD=90°,
由(2)可知∠AFD=∠AFE=∠AGO=45°,
∵∠ADF=90°,
∴AD=DF,设HM=AM=a,则DH=2a,DM=$\sqrt{3}$a,
在Rt△ACD中,∵∠ACD=30°,AD=(1+$\sqrt{3}$)a,
∴CD=BD=$\sqrt{3}$AD=(3+$\sqrt{3}$)a,
在Rt△AHD中,∵∠ADH=30°,AD=(1+$\sqrt{3}$)a,
∴AO=OG=$\frac{1}{2}$AD=$\frac{1+\sqrt{3}}{2}$a,OD=$\sqrt{3}$OA=$\frac{3+\sqrt{3}}{2}$a,
∴OH=OD-DH=$\frac{3+\sqrt{3}}{2}$a-2a=$\frac{\sqrt{3}-1}{2}$a,
∴GH=OG+OH=$\sqrt{3}$a,
∴$\frac{GH}{BD}$=$\frac{\sqrt{3}a}{(3+\sqrt{3})a}$=$\frac{\sqrt{3}-1}{2}$.
点评 本题考查相似三角形综合题、全等三角形的判定和性质、等边三角形的性质、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案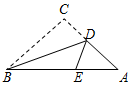 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )cm.
如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )cm.| A. | 9 | B. | 13 | C. | 16 | D. | 10 |
| A. | 4 | B. | 4.5 | C. | 5 | D. | 6 |
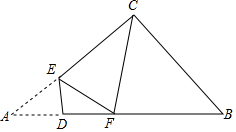 如图,在Rt△ABC中,AC=8,BC=6,点D为斜边AB上一点,DE⊥AB交AC于点E,将△AED沿DE翻折,点A的对应点为点F.如果△EFC是直角三角形,那么AD的长为$\frac{7}{5}$或5.
如图,在Rt△ABC中,AC=8,BC=6,点D为斜边AB上一点,DE⊥AB交AC于点E,将△AED沿DE翻折,点A的对应点为点F.如果△EFC是直角三角形,那么AD的长为$\frac{7}{5}$或5. 已知如图:a∥b,∠2=70°,则∠1=110°,∠3=110°.
已知如图:a∥b,∠2=70°,则∠1=110°,∠3=110°.