题目内容
17.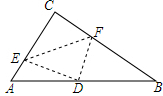 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).若△CEF与△ABC相似.
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).若△CEF与△ABC相似.(1)当AC=BC=2时,求AD的长;
(2)当AC=3,BC=4时,求AD的长.
分析 若△CEF与△ABC相似.
(1)当AC=BC=2时,△ABC为等腰直角三角形;
(2)当AC=3,BC=4时,分两种情况:
a.若CE:CF=3:4,如答图2所示,此时EF∥AB,CD为AB边上的高;
b.若CF:CE=3:4,如答图3所示.由相似三角形角之间的关系,可以推出∠A=∠ECD与∠B=∠FCD,从而得到CD=AD=BD,即D点为AB的中点.
解答 解:(1)若△CEF与△ABC相似.
当AC=BC=2时,△ABC为等腰直角三角形,如答图1所示.
此时D为AB边中点,AD=$\frac{\sqrt{2}}{2}$AC=$\sqrt{2}$;
(2)当AC=3,BC=4时,有两种情况:
a.若CE:CF=3:4,如答图2所示.
∵CE:CF=AC:BC,
∴EF∥AB,
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高.
在Rt△ABC中,AC=3,BC=4,
∴AB=5,
∴cosA=$\frac{3}{5}$.
AD=AC•cosA=3×$\frac{3}{5}$=1.8;
b.若CF:CE=3:4,如答图3所示.
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴此时AD=$\frac{1}{2}$AB=$\frac{1}{2}$×5=2.5.
综上所述,当AC=3,BC=4时,AD的长为1.8或2.5.
点评 本题考查了几何图形折叠问题和相似三角形的判定与性质.第(2)问需要分两种情况分别计算,此处容易漏解,需要引起注意.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
7.某工厂计划本周每日生产30台机器,由于工人实行轮休,每日生产机器的数量不一定相等,实际每日生产量与计划量相比情况如下表(增加的台数为正数,减少的台数为负数)
请解答一下问题:
(1)本周生产了多少台机器?
(2)本周总生产量与计划量相比是增加了还是减少了?增加或减少了多少辆?
(3)生产量最多的一天比生产量最少的一天多生产多少台?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -5 | -2 | +4 | +8 | -7 | -12 |
(1)本周生产了多少台机器?
(2)本周总生产量与计划量相比是增加了还是减少了?增加或减少了多少辆?
(3)生产量最多的一天比生产量最少的一天多生产多少台?
8.正六边形的一个外角的度数为( )
| A. | 120° | B. | 60° | C. | 90° | D. | 100° |
 如图,在平面直角坐标系中,直线AC的表达式为y=-x+6,直线AC与直线OA相交于点A(4,2),有一动点M在线段OA和线段AC上运动.
如图,在平面直角坐标系中,直线AC的表达式为y=-x+6,直线AC与直线OA相交于点A(4,2),有一动点M在线段OA和线段AC上运动.