题目内容
18. 【知识迁移】
【知识迁移】我们知道,函数y=a(x-m)2+n(a≠0,m>0,n>0)的图象是由二次函数y=ax2的图象向右平移m个单位,再向上平移n个单位得到;类似地,函数y=$\frac{k}{x-m}$+n(k≠0,m>0,n>0)的图象是由反比例函数y=$\frac{k}{x}$的图象向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
【理解应用】
函数y=$\frac{3}{x-1}$+1的图象可由函数y=$\frac{3}{x}$的图象向右平移1个单位,再向上平移1个单位得到,其对称中心坐标为(1,1).
【灵活应用】
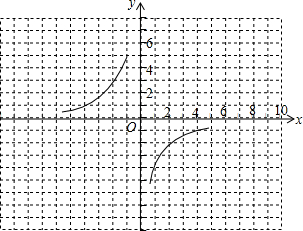
如图,在平面直角坐标系xOy中,请根据所给的y=$\frac{-4}{x}$的图象画出函数y=$\frac{-4}{x-2}$-2的图象,并根据该图象指出,当x在什么范围内变化时,y≥-1?
【实际应用】
某老师对一位学生的学习情况进行跟踪研究,假设刚学完新知识时的记忆存留量为1,新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为y1=$\frac{4}{x+2}$;若在x=t(t≥4)时进行第一次复习,发现他复习后的记忆存留量是复习前的2倍(复习的时间忽略不计),且复习后的记忆存留量随x变化的函数关系为y2=$\frac{4}{x-a}$,如果记忆存留量为$\frac{1}{2}$时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
分析 【理解应用】:根据【知识迁移】得到双曲线的图象平移变换的规律:上加下减.由此得到答案:
【灵活应用】:根据平移规律作出图象;
【实际应用】:先求出第一次复习的“最佳时机点”(6,1),然后代入y2,求出解析式,然后再求出第二次复习的“最佳时机点”.
解答 解:【理解应用】
根据“知识迁移”易得,函数y=$\frac{3}{x-1}$+1的图象可由函数y=$\frac{3}{x}$的图象向右平移1个单位,再向上平移1个单位得到,其对称中心坐标为 (1,1).
故答案是:1,1,(1,1);
【灵活应用】
将y=$\frac{-4}{x}$的图象向右平移2个单位,然后再向下平移两个单位,即可得到函数y=$\frac{-4}{x-2}$-2的图象,其对称中心是(2,-2).图象如图所示:
由y=-1,得$\frac{-4}{x-2}$-2=-1,
解得x=-2.
由图可知,当-2≤x<2时,y≥-1;
【实际应用】
当x=t时,y1=$\frac{4}{t+2}$,
则由y1=$\frac{4}{t+2}$=$\frac{1}{2}$,解得:t=6,
即当t=6时,进行第一次复习,复习后的记忆存留量变为1,
∴点(6,1)在函数y2=$\frac{4}{x-a}$的图象上,
则1=$\frac{4}{6-a}$,解得:a=2,
∴y2=$\frac{4}{x-2}$,
当y2=$\frac{4}{x-2}$=$\frac{1}{2}$,解得:x=10,
即当x=10时,是他第二次复习的“最佳时机点”.
点评 本题主要考查了图象的平移,反比例函数图象的画法和性质,及待定系数法求函数的解析式以及反比例函数的实际应用问题,熟悉反比例函数的图象和性质是解决问题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
13.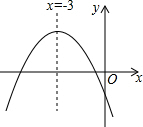 二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )
二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )
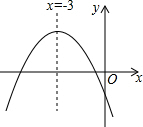 二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )
二次函数y=ax2+bx+c的图象如图所示,已知A(-1,y),B(-4,y2)和C(-5,y3)都在此图象上,下列关系式正确的是( )| A. | y1<y3<y2 | B. | y1>y2>y3 | C. | y3<y2=y1 | D. | y1=y3<y2 |
10.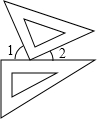 一副三角板按如图方式摆放,且∠1比∠2大50°.若设∠1=x°,∠2=y°,则可得到的方程组为( )
一副三角板按如图方式摆放,且∠1比∠2大50°.若设∠1=x°,∠2=y°,则可得到的方程组为( )
 一副三角板按如图方式摆放,且∠1比∠2大50°.若设∠1=x°,∠2=y°,则可得到的方程组为( )
一副三角板按如图方式摆放,且∠1比∠2大50°.若设∠1=x°,∠2=y°,则可得到的方程组为( )| A. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=180}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=180}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-50}\\{x+y=90}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+50}\\{x+y=90}\end{array}\right.$ |
7. 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )| A. | AB=CD | B. | EC=BF | C. | ∠A=∠D | D. | AB=BC |
8.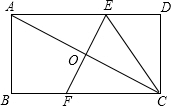 如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
 如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )
如图,在矩形ABCD中,AB=2,BC=4,将矩形沿EF折叠,使点A与点C重合,连接CE,则CE长为( )| A. | 3.5 | B. | 3 | C. | 2.8 | D. | 2.5 |
 如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则
如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.