题目内容
【题目】如图，矩形
中，
，以
为直径作
.
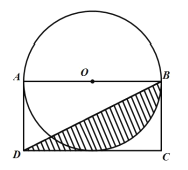
（1）证明:
是的切线；
（2）若
，连接
，求阴影部分的面积.(结果保留
)
【答案】（1）见解析；（2）
【解析】
（1）过O点作OE⊥CD于E点，证四边形OEBC为正方形，可得OE为半径，问题即可得证.
（2）连接BE，S阴影=S△BED+（S扇形OBE-S△BOE），代入数值求解即可.
（1）过O点作OE⊥CD于E点，则∠OEC=90°
∵四边形ABCD为矩形
∴∠ABC=∠BCE=90°
∴四边形OECB为矩形
又AB=2BC，AB=2OB
∴OB=BC
∴四边形OBCE为正方形
∴OE=OB
又OE⊥CD
故CD为
O的切线.
（2）连接BE,
由（1）可得：四边形OBCE为正方形
∴OB=OE=EC=OB=3，DC=AB=6，DE=3
∴S阴影=S△BED+（S扇形OBE-S△BOE）=
练习册系列答案
阅读快车系列答案
相关题目
