Question

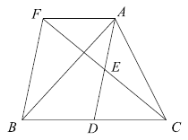
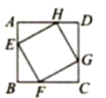
【题目】如图，正方形EFGH的四个顶点分别在正方形ABCD的四条边上，若正方形EFGH与正方形ABCD的相似比为，则（）的值为_____.

Answer 1

【答案】

【解析】

根据题意，由AAS证明△AEH≌△BFE，则BE=AH，根据相似比为，令EH=，AB=，设AE=，AH=，在直角三角形AEH中，利用勾股定理，即可求出的值，即可得到答案.

解：在正方形EFGH与正方形ABCD中，

∠A=∠B=90°，EF=EH，∠FEH=90°，

∴∠AEH+∠AHE=90°，∠BEF+∠AEH=90°，

∴∠AHE=∠BEF，

∴△AEH≌△BFE（AAS），

∴BE=AH，

∵，

令EH=，AB=，

在直角三角形AEH中，设AE=，AH=AB-AE=，

由勾股定理，得，

即，

解得：或，

∵，

∴，

∴，

∴；

故答案为：.