Question

【题目】如图，在正方形ABCD中，E是边CD上一点（点E不与点C，D重合），连接BE．取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．

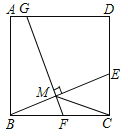
（1）求证：BE＝FG．

（2）连接CM，若CM＝1，试求FG的长．

Answer 1

【答案】（1）详见解析；（2）2．

【解析】

（1）根据正方形的性质可得AB＝BC，∠ABC＝∠BCD＝90°，过点G作GP⊥BC，垂足为P，得矩形ABPG，进而证明△GPF≌△BCE即可得结论；

（2）根据直角三角形斜边上的中线等于斜边的一半即可得FG的长．

（1）证明：如图，

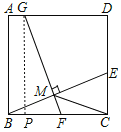
∵四边形ABCD是正方形，

∴AB＝BC，∠ABC＝∠BCD＝90°，

过点G作GP⊥BC，垂足为P，得矩形ABPG，

∴PG＝AB，∠GPF＝90°，

∠PGF+∠GFP＝90°，

∠CBE+∠GFP＝90°，

∴∠PGF＝∠CBE，PG＝CB，∠GPF＝∠BCE＝90°，

∴△GPF≌△BCE（ASA）

∴BE＝FG．

（2）在Rt△BCE中，

∵点M为BE的中点，

∴BE＝2CM，

∴FG＝BE＝2．

答：FG的长为2．