Question

14．请在所给网格中按下列要求操作：
（1）在网格中建立平面直角坐标系，使A点坐标为（-2，3），B点坐标为（4，3），C点坐标为（0，-3）；
（2）求△ABC的面积；
（3）点P在y轴上，当△ABP的面积为6时，请直接写出点P的坐标．

Answer 1

分析 （1）利用A、B点的坐标画出直角坐标系；
（2）利用三角形面积公式求解；
（3）设P（0，t），利用三角形面积公式得到$\frac{1}{2}$•6•|t-3|=6，然后解绝对值方程求出t即可得到P点坐标．

解答 解：（1）如图所示，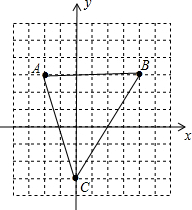

（2）∵A（-2，3）、B（4，3）、C（0，-3），
∴AB=4-（-2）=6，
点C到AB的距离为6，
∴△ABC的面积为：$\frac{1}{2}$6×6=18；
（3）设P（0，t），
根据题意得$\frac{1}{2}$•6•|t-3|=6，解得t=1或t=5，
所以P点的坐标为（0，1）或（0，5）．

点评 本题考查了坐标与图形性质：利用点的坐标进行相应线段的长和判断线段与坐标轴的位置关系．