题目内容
6. 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF.(1)若AB=6,求CD的长;
(2)求证:OA2=OE•OF.
分析 (1)由EC∥AB,∠EDA=∠ABF,可证得∠DAB=∠ABF,即可证得AD∥BC,则得四边形ABCD为平行四边形,于是得到结论;
(2)由EC∥AB,可得$\frac{OA}{OE}$=$\frac{OB}{OD}$,由AD∥BC,可得$\frac{OB}{OD}$=$\frac{OF}{OA}$,等量代换得出$\frac{OA}{OE}$=$\frac{OF}{OA}$,即OA2=OE•OF.
解答 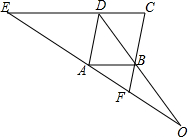 证明:(1)∵EC∥AB,
证明:(1)∵EC∥AB,
∴∠EDA=∠DAB,
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD∥BC,
∵DC∥AB,
∴四边形ABCD为平行四边形,
∴CD=AB=6;
(2)∵EC∥AB,
∴△OAB∽△OED,
∴$\frac{OA}{OE}$=$\frac{OB}{OD}$,
∵AD∥BC,
∴△OBF∽△ODA,
∴$\frac{OB}{OD}$=$\frac{OF}{OA}$,
∴$\frac{OA}{OE}$=$\frac{OF}{OA}$,
∴OA2=OE•OF.
点评 此题考查了相似三角形的判定与性质,平行四边形的判定,平行线的性质,解题时要注意识图,灵活应用数形结合思想.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
14.已知某种商品的标价为200元,即使搞促销活动打九折后仍有20%的利润,则该商品的成本价是( )
| A. | 144元 | B. | 150元 | C. | 153元 | D. | 167元 |
18.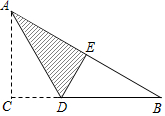 如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )
如图,△ABC中,∠C=90°,AC=6,BC=8,点D在BC上,沿AD折叠使点C落在AB上的点E,设BD=x,则可得方程( )| A. | x2=(8-x)2+62 | B. | x2=(8-x)2+42 | C. | x=8-x+4 | D. | x2=62+82 |
 如图,在七巧板中找出一组互相平行的线段GL∥BC和一组互相垂直的线段EK⊥AC.
如图,在七巧板中找出一组互相平行的线段GL∥BC和一组互相垂直的线段EK⊥AC. 如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0),直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F.
如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0),直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F.
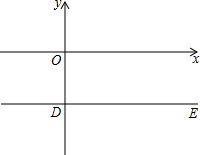 已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.
已知:直线l:y=2x+2b与过点D(0,-2)平行于x轴的直线DE交于B点,与x轴交于点A.