题目内容
17.计算:(1)($\sqrt{\frac{9}{2}}$$-\frac{\sqrt{98}}{3}$)×2$\sqrt{2}$
(2)$\sqrt{48}$$÷\sqrt{3}$$-\sqrt{\frac{1}{2}}$×$\sqrt{12}$$+\sqrt{24}$.
分析 (1)先把二次根式化为最简二次根式,然后进行二次根式的乘法运算;
(2)先进行二次根式的乘除运算,然后化简后合并即可.
解答 解:(1)原式=($\frac{3\sqrt{2}}{2}$-$\frac{7\sqrt{2}}{3}$)×2$\sqrt{2}$
=$\frac{3\sqrt{2}}{2}$×$2\sqrt{2}$-$\frac{7\sqrt{2}}{3}$×2$\sqrt{2}$
=6-$\frac{28}{3}$
=-$\frac{10}{3}$;
(2)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
8.根据下列表述,能确定位置的是( )
| A. | 国际影城3排 | B. | A市南京路口 | ||
| C. | 北偏东60° | D. | 东经100°,北纬30° |
9.下列说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 1是最小的正数 | ||
| C. | 一个有理数不是整数就是分数 | D. | 与0具有相反意义的量是0 |
 如图,一个正方体的平面展开图,若图中平面展开图折叠成正方体后,相对面上的两个数字之和均为5,求x+y+z的值.
如图,一个正方体的平面展开图,若图中平面展开图折叠成正方体后,相对面上的两个数字之和均为5,求x+y+z的值.
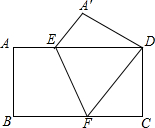 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.