题目内容
19.若关于x不等式组$\left\{\begin{array}{l}{3x-2>0}\\{-x+m≥7}\end{array}\right.$无公共解集,则m的取值范围是m≤$\frac{23}{3}$.分析 根据不等式组无解,可得答案.
解答 解:由3x-2>0,解得x>$\frac{2}{3}$,
由-x+m≥7解得x≤m-7.
由不等式组无解,得
m-7≤$\frac{2}{3}$,
解得m≤$\frac{23}{3}$,
故答案为:m≤$\frac{23}{3}$.
点评 本题考察了不等式的解集,利用不等式组无解得出关于m的不等式是解题关键.

练习册系列答案
相关题目
9.原价为100元的某种药品经过连续两次降价后为64元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
| A. | 100(1-x)2=64 | B. | 64(1-x)2=100 | C. | 100(1-2x)=64 | D. | 64(1-2x)=100 |
10.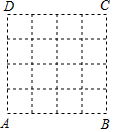 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.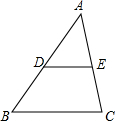 如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
 如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )| A. | $\frac{5}{6}$ | B. | $\frac{5}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
1.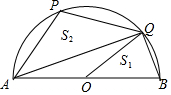 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
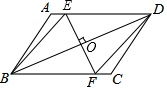 如图,在平行四边形ABCD中,点O是对角线BD的中点,过O点作EF⊥BD,交AD于E,交BC于F,那么,四边形EBFD是菱形吗?为什么?
如图,在平行四边形ABCD中,点O是对角线BD的中点,过O点作EF⊥BD,交AD于E,交BC于F,那么,四边形EBFD是菱形吗?为什么?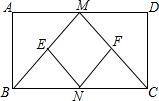 如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点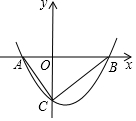 平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.
平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.