题目内容
如图，等腰直角三角形放置在两平行直线m、n上，与直线m相交成∠1=120°，那么与直线n相交成的∠2等于（ ）| A、30° | B、45° |
| C、60° | D、75° |
考点：平行线的性质,等腰直角三角形
专题：
分析：根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠3，再根据两直线平行，同位角相等可得∠4=∠3，然后根据对顶角相等解答．
解答：
解：由三角形的外角性质得，
∠3=∠1-45°=120°-45°=75°，
∵m∥n，
∴∠4=∠3=75°（两直线平行，同位角相等），
∴∠2=∠4=75°（对顶角相等）．
故选：D．
解：由三角形的外角性质得，∠3=∠1-45°=120°-45°=75°，
∵m∥n，
∴∠4=∠3=75°（两直线平行，同位角相等），
∴∠2=∠4=75°（对顶角相等）．
故选：D．
点评：本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，平行线的性质，熟记性质并准确识图是解题的关键．
练习册系列答案
相关题目
下列说法：
①负数没有平方根；
②任何一个数的平方根都有2个，它们互为相反数；
③无理数是无限不循环小数；
④
的平方根是3．
其中错误的有（ ）
①负数没有平方根；
②任何一个数的平方根都有2个，它们互为相反数；
③无理数是无限不循环小数；
④
| 9 |
其中错误的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
小兰画了一个函数y=x2+ax+b的图象如图，则关于x的方程x2+ax+b=0的解是（ ）| A、无解 | B、x=1 |
| C、x=-4 | D、x=-1或x=4 |
正方形的边长是1，它的对角线长为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，则二楼的层高BC约为（精确到0.1米，sin42°≈0.67，tan42°≈0.90）（ ）
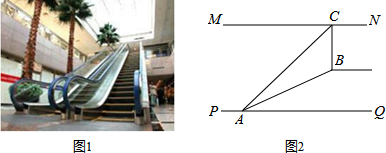
| A、10.8米 | B、8.9米 |
| C、8.0米 | D、5.8米 |
已知a＜b，则下列四个不等式中，不正确的是（ ）
| A、a-2＜b-2 |
| B、a-b＜0 |
| C、2a＞a+b |
| D、-2a＞-2b |
计算-[-（-a）3]2•（
）-2结果为（ ）
| 1 |
| 3 |
A、
| ||
B、
| ||
| C、-9a6 | ||
D、-
|