题目内容
 你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.
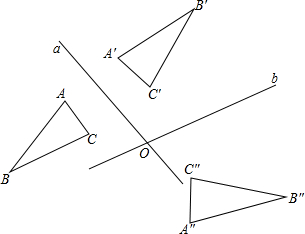
你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.假如把这两条平行直线换成相交直线,又能得到什么结论呢?如图,已知△ABC,直线a、b相交于点O,请先画出△ABC关于直线a对称的△A′B′C′,然后画出△A′B′′C关于直线b对称的△A″B″C″,你能发现ABC和A″B″C″有什么关系吗?
猜想:在此图中,若再增加什么条件,能使得△ABC△A″B″C″关于点O成中心对称呢?
考点:中心对称
专题:
分析:由轴对称的性质可得OA=OA′=OA″,再根据旋转的性质解答即可;
根据中心对称的性质可得OA=OA″,根据轴对称的性质可得OA=OA′=OA″,然后判断出△AA′A″是直角三角形,AA′⊥A′A″,再根据轴对称的性质判断即可.
根据中心对称的性质可得OA=OA″,根据轴对称的性质可得OA=OA′=OA″,然后判断出△AA′A″是直角三角形,AA′⊥A′A″,再根据轴对称的性质判断即可.
解答:解:∵∵△ABC关于直线a对称的△A′B′C′,然后画出△A′B′C′关于直线b对称的△A″B″C″,
∴OA=OA′=OA″,
∴△ABC绕两直线的交点旋转得到△A″B″C″;
猜想:添加条件为a⊥b.
理由如下:∵△ABC与△A″B″C″关于点O成中心对称,
∴OA=OA″,
∵△ABC关于直线a对称的△A′B′C′,然后画出△A′B′C′关于直线b对称的△A″B″C″,
∴OA=OA′=OA″,
∴△AA′A″是直角三角形,
∴AA′⊥A′A″,
由轴对称的性质,AA′⊥a,A′A″⊥b,
∴a⊥b.
∴OA=OA′=OA″,
∴△ABC绕两直线的交点旋转得到△A″B″C″;
猜想:添加条件为a⊥b.
理由如下:∵△ABC与△A″B″C″关于点O成中心对称,
∴OA=OA″,
∵△ABC关于直线a对称的△A′B′C′,然后画出△A′B′C′关于直线b对称的△A″B″C″,
∴OA=OA′=OA″,
∴△AA′A″是直角三角形,
∴AA′⊥A′A″,
由轴对称的性质,AA′⊥a,A′A″⊥b,
∴a⊥b.
点评:本题考查了中心对称的性质,轴对称的性质,熟记各性质并判断出对应顶点构成的三角形是直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题: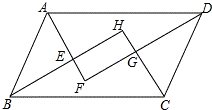 如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论.
如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论. 如图,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?
如图,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?