题目内容
11. 如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.(1)求证:DE是⊙O的切线;
(2)当DE=1,∠C=30°时,求图中阴影部分的面积.
分析 (1)连接OD,利用平行线的判定定理可以得到∠ODE=∠DEC=90°,从而判断DE是圆的切线;
(2)由∠C=30°,DE=1,∠DEC=90°,求得DC=2,由于OD∥BC,于是得到∠ODA=30°,根据等腰三角形的性质得到∠AOD=120°,于是得到OA=$\frac{2\sqrt{3}}{3}$,阴影部分面积即可求得.
解答 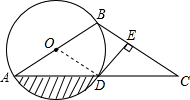 解:(1)连接OD,
解:(1)连接OD,
∵AB是⊙O的直径,D是AC的中点,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∵点D在圆上,
∴DE为⊙O的切线;
(2)∵∠C=30°,DE=1,∠DEC=90°,
∴DC=2,
∵OD∥BC,
∴∠ODA=30°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∴∠AOD=120°,
∴OA=$\frac{2\sqrt{3}}{3}$,
∴阴影部分面积S=$\frac{120•π×(\frac{2\sqrt{3}}{3})^{2}}{360}$-$\frac{1}{2}$×2×$\frac{\sqrt{3}}{3}$=$\frac{4π}{9}$-$\frac{\sqrt{3}}{3}$.
点评 本题目考查了切线的判定,等腰三角形的判定及性质、圆周角定理及切线的性质,涉及的知识点比较多且碎,解题时候应该注意.

练习册系列答案
相关题目
3.已知点A(-2,1),B(1,4),若反比例函数y=$\frac{k}{x}$与线段AB有公共点时,k的取值范围是( )
| A. | -$\frac{9}{4}$≤k<0或0<k≤4 | B. | k≤-2或k≥4 | C. | -2≤k<0或k≥4 | D. | -2≤k<0或0<k≤4 |
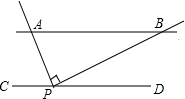 如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=65度.
如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=65度. 如图,将平面直角坐标系的纵轴绕原点顺时针旋转30°,得到夹角为60°的平面坐标系xOy,称之为平面60°角坐标系.类比平面直角坐标系中确定点的坐标的方法,设平面60°角坐标系中有任意一点P,过点P作PA∥y轴,交x轴于点A,A点的坐标为(x,0),过点P作PB∥x轴,交y轴于点B,B点的坐标为(0,y),则点P坐标为(x,y).
如图,将平面直角坐标系的纵轴绕原点顺时针旋转30°,得到夹角为60°的平面坐标系xOy,称之为平面60°角坐标系.类比平面直角坐标系中确定点的坐标的方法,设平面60°角坐标系中有任意一点P,过点P作PA∥y轴,交x轴于点A,A点的坐标为(x,0),过点P作PB∥x轴,交y轴于点B,B点的坐标为(0,y),则点P坐标为(x,y).