题目内容
1.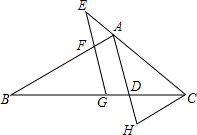 如图,在△ABC中,G为BC的中点,E为CA延长线上一点,EG交AB于F,AD∥EG交BC于点D,CH∥AB交AD延长线于点H,且EC=k•AC,探究:FB与CH的数量关系.
如图,在△ABC中,G为BC的中点,E为CA延长线上一点,EG交AB于F,AD∥EG交BC于点D,CH∥AB交AD延长线于点H,且EC=k•AC,探究:FB与CH的数量关系.
分析 由已知条件得到△ACD∽△CEG,证得$\frac{GC}{CD}$=$\frac{EC}{AC}$=k,推出$\frac{BG}{CD}$=k,由△BFG∽△BAD,△CHD∽△BAD,得到△BFG∽△CHD,根据相似三角形的性质即可得到结论.
解答 解:∵AD∥EG,
∴△ACD∽△CEG,
∴$\frac{EC}{AC}=\frac{GC}{CD}$,
∵EC=k•AC,
∴$\frac{GC}{CD}$=$\frac{EC}{AC}$=k,
∵G为BC的中点,
∴BG=CG,
∴$\frac{BG}{CD}$=k,
∵GE∥AD,
∴△BFG∽△BAD,
∵CH∥AB,
∴△CHD∽△BAD,
∴△BFG∽△CHD,
∴$\frac{BF}{CH}=\frac{BG}{CD}$=k,
∴BF=k•CH.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
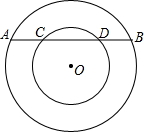 如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,若AB=10cm,CD=6cm.
如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,若AB=10cm,CD=6cm. 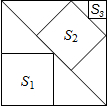 如图,边长为18的大正方形中有三个小正方形,若三个小正方形的面积分别为S1、S2、S3,则S1+S2+S3的值162.
如图,边长为18的大正方形中有三个小正方形,若三个小正方形的面积分别为S1、S2、S3,则S1+S2+S3的值162.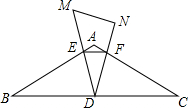 已知△ABC中,AB=AC=8,∠B=30°,D为BC上中点,Rt△DNM中,∠MDN=30°,D为定点,DM、DN交AB、AC于E、F.
已知△ABC中,AB=AC=8,∠B=30°,D为BC上中点,Rt△DNM中,∠MDN=30°,D为定点,DM、DN交AB、AC于E、F.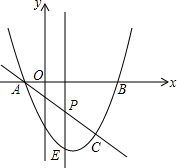 如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.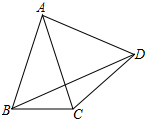 如图,△ABC中,AB=AC,∠BAC=40°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是20°,80°,200°,320°.
如图,△ABC中,AB=AC,∠BAC=40°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是20°,80°,200°,320°.