题目内容
14.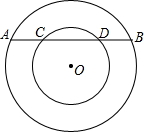 如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,若AB=10cm,CD=6cm.
如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,若AB=10cm,CD=6cm. (1)求AC的长;
(2)若大圆半径为13cm,求小圆的半径.
分析 (1)作出弦心距OE,垂足为E,根据垂径定理可以求出AE、CE的长,再由AC=AE-CE即可得出结论;
(2)连接OA,OC,根据勾股定理求出OE的长,再在Rt△OCE中利用勾股定理即可得出OC的长.
解答 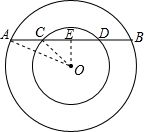 解:(1)作OE⊥AB,垂足为E,由垂径定理知,点E是CD的中点,也是AB的中点
解:(1)作OE⊥AB,垂足为E,由垂径定理知,点E是CD的中点,也是AB的中点
∴AE=$\frac{1}{2}$AB=5,CE=$\frac{1}{2}$CD=3
∴AC=AE-CE=5-3=2cm;
(2)连接OA,OC,
∵在Rt△AOE中,AE=5cm,OA=13cm,
∴OE=$\sqrt{{OA}^{2}-{AE}^{2}}$=$\sqrt{{13}^{2}-{5}^{2}}$=12cm.
在Rt△OCE中,
∵CE=3cm,OE=12cm,
∴OC=$\sqrt{{OE}^{2}+{CE}^{2}}$=$\sqrt{{12}^{2}+{3}^{2}}$=5$\sqrt{6}$(cm).
点评 本题考查的是垂径定理,根据题意作出辅助线,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
4.奉节特产专卖店销售2015年良种夏季脐橙,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克.若该专卖店销售这种脐橙要想平均每天获利2240元,为减少库存,每千克脐橙应降价多少元?( )
| A. | 4元 | B. | 6元 | C. | 4元或6元 | D. | 5元 |
19.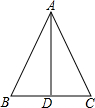 下列条件中能使△ABD≌△ACD的是( )
下列条件中能使△ABD≌△ACD的是( )
 下列条件中能使△ABD≌△ACD的是( )
下列条件中能使△ABD≌△ACD的是( )| A. | AB=AC,∠B=∠C | B. | AB=AC,∠ADB=∠ADC | C. | AB=AC,∠BAD=∠CAD | D. | BD=CD,∠BAD=∠CAD |
3.-3减去-$\frac{7}{5}$与-$\frac{3}{5}$的和的结果是( )
| A. | -$\frac{19}{5}$ | B. | -$\frac{11}{5}$ | C. | -5 | D. | -1 |
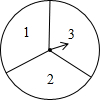 2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.
2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.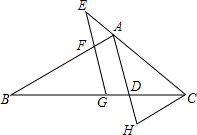 如图,在△ABC中,G为BC的中点,E为CA延长线上一点,EG交AB于F,AD∥EG交BC于点D,CH∥AB交AD延长线于点H,且EC=k•AC,探究:FB与CH的数量关系.
如图,在△ABC中,G为BC的中点,E为CA延长线上一点,EG交AB于F,AD∥EG交BC于点D,CH∥AB交AD延长线于点H,且EC=k•AC,探究:FB与CH的数量关系.