题目内容
 如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.
如图,AD为⊙O的直径,AB、AC为弦,且AD平分∠BAC,试判定AB与AC的关系,并证明你的结论.考点:垂径定理,角平分线的性质
专题:
分析:连接BC,根据AD平分∠BAC可知
=
,进而可得出AD是弦BC的垂直平分线,再根据ASA定理可得出△ABM≌△ACM,由此即可得出结论.
 |
| BD |
 |
| CD |
解答: 解:AB=AC.
解:AB=AC.
理由:连接BC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴
=
,
∵AD是⊙O的直径,
∴AD⊥BC,BM=CM,
在△ABM与△ACM中,
∵
,
∴△ABM≌△ACM,
∴AB=AC.
 解:AB=AC.
解:AB=AC.理由:连接BC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| CD |
∵AD是⊙O的直径,
∴AD⊥BC,BM=CM,
在△ABM与△ACM中,
∵
|
∴△ABM≌△ACM,
∴AB=AC.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
在平行四边形ABCD中,∠A=2∠B,则∠C的度数是( )
| A、60° | B、90° |
| C、120° | D、135° |
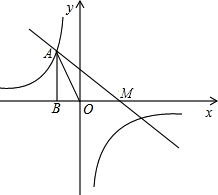 如图,已知反比例函数y=
如图,已知反比例函数y=