题目内容
1．
如图是一个矩形的储物柜，它被分成4个大小不同的正方形①②③④和一个矩形⑤，若要计算⑤的周长，则只需要知道哪个小正方形的周长？你的选择是（ ）| A． | ① | B． | ② | C． | ③ | D． | ④ |
分析 记正方形①②③④的边长分别为a、b、c、d．则矩形的周长=2[d+a+（b-a））]，由c=a+b=d-a等量代换即可解决问题．
解答 解：记正方形①②③④的边长分别为a、b、c、d．
则矩形⑤的周长=2[d+a+（b-a））]，
因为c=a+b=d-a，
所以矩形⑤的周长=2[d+a+（b-a））]=2[（d-a）+（a+b）]=2（2a+2b）=4（a+b）=4c．
所以只要知道③的边长即可计算⑤的周长．
故选C．
点评 本题考查矩形的性质、周长等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
练习册系列答案
相关题目
16．
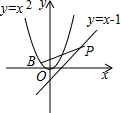如图，点P在直线y=x-1上，若存在过点P的直线交抛物线y=x2于A、B两点，且PA=AB，则称点P为“优点”，下列结论中正确的是（ ）
如图，点P在直线y=x-1上，若存在过点P的直线交抛物线y=x2于A、B两点，且PA=AB，则称点P为“优点”，下列结论中正确的是（ ）| A． | 直线y=x-1上的所有点都是“优点” | |
| B． | 直线y=x-1上仅有有限个点是“优点” | |
| C． | 直线y=x-1上的所有点都不是“优点” | |
| D． | 直线y=x-1上有无穷多个点（不是所有的点）是“优点” |
已知如图所示△ABC中，∠ACB=90°，AC=BC，点P在△ABC内，且PA=$\sqrt{3}$，PB=1，PC=1，则∠BPC=135°．
一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，BC=10$\sqrt{3}$，试求CD的长．