题目内容
3.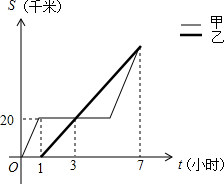 甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:
甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:(1)A、B两地相距60千米,乙骑自行车的速度为10千米/时,甲因事耽误了4小时
(2)求出甲、乙两人在途中相遇以后,距离甲出发多长时间甲、乙两人相距5千米?
分析 观察图象可得A、C两地相距20千米,乙的时间为2小时,得出速度,再得出AB之间的距离;甲比乙早1小时出发到达C地,得出甲的速度后,然后得出甲的速度,最后根据此信息进行分析即可.
解答 解:(1)由图象可得:
A、C两地相距20千米,乙的时间为(3-1)=2小时,
可得:乙的速度为:20÷2=10千米/小时,
因为AB两地乙所用时间为(7-1)=6小时,
所以AB两地的距离为:6×10=60千米;
由图象可得:
A、C两地相距20千米,甲的时间为(1-0)=1小时,
可得:甲的速度为:20÷1=20千米/小时,
从C地到达B地的距离为:60-20=40千米,
所以甲从C地到达B地的时间为:40÷20=2小时;
所以甲因事耽误的时间为:7-1-2=4小时;
故答案为:60;10;4;
(2)甲、乙两人在途中相遇以后,当乙比甲多5千米时,可得乙从C地出发的时间为:5÷10=0.5小时,
此时甲仍在C地,可得甲、乙两人在途中相遇以后,甲、乙两人相距5千米,甲出发的时间为3+0.5=3.5小时.
点评 本题考查了函数图象:学会看函数图象,理解函数图象所反映的实际意义,从函数图象中获取信息,并且解决有关问题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
13.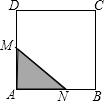 如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )
如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )
 如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )
如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )| A. | 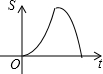 | B. | 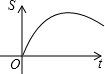 | C. | 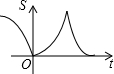 | D. | 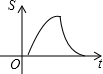 |
14.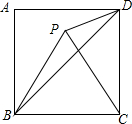 如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )
如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )
 如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )
如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )| A. | $\sqrt{7-4\sqrt{3}}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | $\sqrt{8-4\sqrt{3}}$ |
18.下列各式中正确的是( )
| A. | 若a>b,则a-1<b-1 | B. | 若a>b,则a2>b2 | ||
| C. | 若a>b,且c≠0,则ac>bc | D. | 若$\frac{a}{|c|}$>$\frac{b}{|c|}$,则a>b |
8.氢原子中电子和原子核之间的距离为0.00000000529厘米,用科学记数法表示这个距离为( )
| A. | 5.29×10-8cm | B. | 5.29×10-9cm | C. | 0.529×10-8cm | D. | 52.9×10-10cm |
13.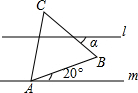 如图,l∥m,等边△ABC的顶点A在m上,则∠α的度数为( )
如图,l∥m,等边△ABC的顶点A在m上,则∠α的度数为( )
 如图,l∥m,等边△ABC的顶点A在m上,则∠α的度数为( )
如图,l∥m,等边△ABC的顶点A在m上,则∠α的度数为( )| A. | 20° | B. | 40° | C. | 50° | D. | 60° |