题目内容
14.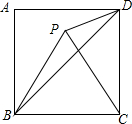 如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )
如图,已知正方形ABCD的边长为2,以C点为圆心将线段BC顺时针旋转60°,连接BP.PD,则PD的长是( )| A. | $\sqrt{7-4\sqrt{3}}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-2 | D. | $\sqrt{8-4\sqrt{3}}$ |
分析 过点P作PE⊥CD于E,根据四边形ABCD是正方形,∠BCP=60°,得出∠PCD=30°,DC=PC=2,再分别求出PE、CE,再求出DE,最后根据PD=$\sqrt{P{E}^{2}+D{E}^{2}}$代入计算即可.
解答 解:过点P作PE⊥CD于E,
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD=2,
∵∠BCP=60°,BC=PC,
∴∠PCD=30°,DC=PC=2,
∴PE=$\frac{1}{2}$PC=1,
∴CE=$\sqrt{P{C}^{2}-P{E}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴DE=2-$\sqrt{3}$,
∴PD=$\sqrt{P{E}^{2}+D{E}^{2}}$=$\sqrt{{1}^{2}+(2-\sqrt{3})^{2}}$=$\sqrt{8-4\sqrt{3}}$,
故选:D.
点评 此题考查了旋转的性质,用到的知识点是正方形的性质、旋转的性质、勾股定理,关键是作出辅助线,构造直角三角形.

练习册系列答案
相关题目
9.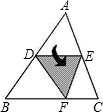 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
 如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )
如图,D、E为△ABC两边AB、AC上的两点,将△ABC沿线段DE折叠,使得DE∥BC,且点A落在点F处,若∠B=55°,则∠BDF为( )| A. | 55° | B. | 60° | C. | 70° | D. | 不能确定 |
6.“大嘴猴”童装店最近销售了某种夏装30件,销售量如下表所示:则所销售夏装尺码的中位数是( )
| 尺码(厘米) | 100 | 105 | 110 | 115 | 120 | 125 | 130 |
| 销售量(件) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
| A. | 105 | B. | 110 | C. | 115 | D. | 120 |
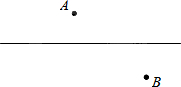 如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?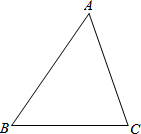 按要求在图中画图,并把答案填写在横线上.
按要求在图中画图,并把答案填写在横线上.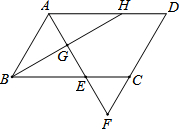 如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.
如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.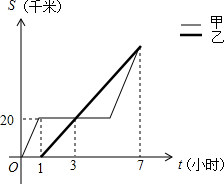 甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:
甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题: