题目内容
9.$\sqrt{11}$的整数部分为a,小数部分为b,则a+b2的值为23-6$\sqrt{11}$.分析 先依据被开放数越大对应的算术平方根越大估算出$\sqrt{11}$的大致范围,从而可得到a、b的值,最后代入计算即可.
解答 解:∵9<11<16,
∴3<$\sqrt{11}$<4.
∴a=3,b=$\sqrt{11}$-3.
∴a+b2=3+($\sqrt{11}$-3)2=3+11+9-6$\sqrt{11}$=23-6$\sqrt{11}$.
故答案为:23-6$\sqrt{11}$.
点评 本题主要考查的是估算无理数的大小,熟练掌握估算无理数大小的方法是解题的关键.

练习册系列答案
相关题目
20. 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )
 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )| A. |  | B. |  | C. |  | D. |  |
17.下列运算结果正确的是( )
| A. | a3+a4=a7 | B. | a4÷a3=a | C. | a3•a2=2a3 | D. | (a3)3=a6 |
14.下表为我省大同市5个空气质量监测站点对某日空气中PM2.5浓度(单位:μg/m3)的检测数据,则这组数据的中位数为( )
| 检测站点 | 果树杨 | 云冈宾馆 | 大同大学 | 安家小村 | 教育学院 |
| PM2.5浓度 | 76μg/m3 | 80μg/m3 | 97μg/m3 | 94μg/m3 | 93μg/m3 |
| A. | 97μg/m3 | B. | 80μg/m3 | C. | 94μg/m3 | D. | 93μg/m3 |
 如图,菱形ABCD中,∠BCD=120°,AC=5,则菱形ABCD的周长是20.
如图,菱形ABCD中,∠BCD=120°,AC=5,则菱形ABCD的周长是20.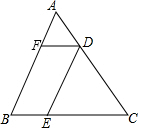 如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.
如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( ) 如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.