题目内容
若x1、x2是方程x2-(m+2)x+m2=0的两个实数根,且满足x1x2=x1+x2,则m的值是( )
| A、-1或2 | B、2 |
| C、-1 | D、1或-2 |
考点:根与系数的关系
专题:计算题
分析:根据根与系数的关系得到x1+x2=m+2,x1x2=m2,由x1x2=x1+x2得到m2=m+2,再解方程得到m1=2,m2=-1,然后根据根的判别式确定满足条件的m的值.
解答:解:根据题意得x1+x2=m+2,x1x2=m2,
∵x1x2=x1+x2,
∴m2=m+2,
整理得m2-m-2=0,解得m1=2,m2=-1,
∵m=-1时,原方程变形为x2-x+1=0,△<0,此方程没有实数解,
∴m的值为2.
故选B.
∵x1x2=x1+x2,
∴m2=m+2,
整理得m2-m-2=0,解得m1=2,m2=-1,
∵m=-1时,原方程变形为x2-x+1=0,△<0,此方程没有实数解,
∴m的值为2.
故选B.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、等边三角形 | B、平行四边形 |
| C、正五边形 | D、菱形 |
在平面直角坐标系xOy中,以M(3,4)为圆心,半径为5的圆与x轴的位置关系是( )
| A、相离 | B、相交 |
| C、相切 | D、无法确定 |
 如图,已知∠1=∠2,CF⊥AB于F,DE⊥AB于E,则FP与BC平行吗?
如图,已知∠1=∠2,CF⊥AB于F,DE⊥AB于E,则FP与BC平行吗?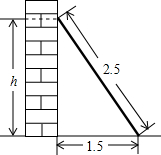 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h.