题目内容
2.若$\sqrt{{x}^{3}+3{x}^{2}}$=-x$\sqrt{x+3}$,则x的取值范围是( )| A. | x≥-3 | B. | x≤0 | C. | x>3 | D. | -3≤x≤0 |
分析 根据二次根式的性质、二次根式有意义的条件列出不等式,解不等式即可.
解答 解:∵$\sqrt{{x}^{3}+3{x}^{2}}$=|x|$\sqrt{x+3}$=-x$\sqrt{x+3}$,x+3≥0,
∴x≤0,x≥-3,
则x的取值范围是-3≤x≤0,
故选:D.
点评 本题考查的是二次根式的化简、二次根式有意义的条件,掌握二次根式的性质、二次根式被开方数是非负数是解题的关键.

练习册系列答案
相关题目
12. 如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
 如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )| A. | AB=AC | B. | BD=CD | C. | ∠BDA=∠CDA | D. | ∠B=∠C |
13. “天宫二号”是中国载人航天工程中第一个真正意义上的空间实验室,2016年9月15日,“天宫二号”发射取得圆满成功,它的运行轨道距离地球393000米,数据393000米用科学记数法表示为( )
“天宫二号”是中国载人航天工程中第一个真正意义上的空间实验室,2016年9月15日,“天宫二号”发射取得圆满成功,它的运行轨道距离地球393000米,数据393000米用科学记数法表示为( )
 “天宫二号”是中国载人航天工程中第一个真正意义上的空间实验室,2016年9月15日,“天宫二号”发射取得圆满成功,它的运行轨道距离地球393000米,数据393000米用科学记数法表示为( )
“天宫二号”是中国载人航天工程中第一个真正意义上的空间实验室,2016年9月15日,“天宫二号”发射取得圆满成功,它的运行轨道距离地球393000米,数据393000米用科学记数法表示为( )| A. | 0.393×107米 | B. | 3.93×106米 | C. | 3.93×105米 | D. | 39.3×104米 |
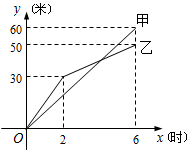 有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.如图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.如图是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题: 如果一个等腰三角形的底边与腰的比值为m,而且m恰好是一元二次方程x2+x-1=0的正根,我们称这样等腰三角形为“黄金三角形”.已知等腰三角形ABC是黄金三角形,AB、AC是腰,延长BC到D,使得CD等于AC,连结AD,图中还有黄金三角形吗?有,请找出,并说明理由.
如果一个等腰三角形的底边与腰的比值为m,而且m恰好是一元二次方程x2+x-1=0的正根,我们称这样等腰三角形为“黄金三角形”.已知等腰三角形ABC是黄金三角形,AB、AC是腰,延长BC到D,使得CD等于AC,连结AD,图中还有黄金三角形吗?有,请找出,并说明理由.