题目内容
1.已知:x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$,求x4+y4的值.分析 首先化简x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=5+2$\sqrt{6}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=5-2$\sqrt{6}$,进一步利用完全平方公式整理代数式代入求得答案即可.
解答 解:∵x=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=5+2$\sqrt{6}$,y=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=5-2$\sqrt{6}$,
∴x4+y4
=(x2+y2)2-2x2y2
=[(5+2$\sqrt{6}$)2+(5-2$\sqrt{6}$)2]2-2[(5+2$\sqrt{6}$)(5-2$\sqrt{6}$)]2
=(49+20$\sqrt{6}$+49-20$\sqrt{6}$)2-2
=982-2
=9602.
点评 此题考查二次根式的化简求值,掌握化简的方法以及完全平方公式是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | π | D. | $\frac{1}{7}$ |
9.一个等腰三角形的两个内角和为100°,则它的顶角度数为( )
| A. | 50° | B. | 80° | C. | 50°或80° | D. | 20°或80° |
13.九年级11个班中开展篮球单循环比赛(每班需进行10场比赛),比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得-1分,已知(2)班在所有的比赛中得到14分.若设该班胜x场,则x应满足的方程是( )
| A. | 3x+(10-x)=14 | B. | 3x-(10-x)=14 | C. | 3x+x=14 | D. | 3x-x=14 |
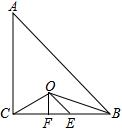 Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为8.
Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为8.