题目内容
12.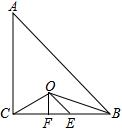 Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为8.
Rt△ABC中,AC=BC,∠ACB=90°,如图,BO、CO分别平分∠ABC、∠ACB,EO∥AB,FO∥AC,若S△ABC=32,则△OEF的周长为8.
分析 根据已知条件得到BC=8,根据平行线的性质得到∠ABO=∠BOE由角平分线的定义得到∠ABOE=∠OBE,等量代换得到∠ABO=∠BOE于是得到BE=OE,则同理可得CE=OE即可得到结论.
解答 解:∵AC=BC,∠ACB=90°,S△ABC=32,
∴$\frac{1}{2}$BC2=32,
∴BC=8,
∵OED∥AB
∴∠ABO=∠BOE
∵OB平分∠ABC
∴∠ABOE=∠OBE
∴∠ABO=∠BOE
∴BE=OE,
则同理可得CE=OE
∴△OEF的周长=OE+OF+EF=BE+EF+FC=BC=8.
故答案为:8.
点评 本题主要考查了三角形的面积,平行线的判定和性质,角平分线的性质,等腰三角形的性质和判断,能灵活应用角平分线的定义,平行线及等腰三角形的性质是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7. 如图,CD⊥AB于D,BE⊥AC于E,BE与CD交于O,OB=OC,则图中全等三角形共有( )
如图,CD⊥AB于D,BE⊥AC于E,BE与CD交于O,OB=OC,则图中全等三角形共有( )
 如图,CD⊥AB于D,BE⊥AC于E,BE与CD交于O,OB=OC,则图中全等三角形共有( )
如图,CD⊥AB于D,BE⊥AC于E,BE与CD交于O,OB=OC,则图中全等三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
 如图,OB、OC是⊙O的半径,A是⊙O上的一点,若∠B=30°,∠C=20°,则△BAC=50°.
如图,OB、OC是⊙O的半径,A是⊙O上的一点,若∠B=30°,∠C=20°,则△BAC=50°.