题目内容
已知|a|=4,b2=9且|a+b|≠a+b,则代数式a-b的值为( )
| A、1或7 | B、1或-7 |
| C、-1或-7 | D、±1或±7 |
考点:代数式求值
专题:
分析:根据绝对值的性质和有理数的乘方求出a、b,然后判断出a、b的对应情况,再代入代数式计算即可得解.
解答:解:∵|a|=4,b2=9,
∴a=±4,b=±3,
∵|a+b|≠a+b,
∴a+b<0,
∴a=-4,b=±3,
∴a-b=-4-3=-7,
或a-b=-4-(-3)=-4+3=-1,
综上所述,a-b=-1或-7.
故选C.
∴a=±4,b=±3,
∵|a+b|≠a+b,
∴a+b<0,
∴a=-4,b=±3,
∴a-b=-4-3=-7,
或a-b=-4-(-3)=-4+3=-1,
综上所述,a-b=-1或-7.
故选C.
点评:本题考查了代数式求值,主要利用了绝对值的性质,有理数的乘方,熟记性质并确定出a、b的值是解题的关键.

练习册系列答案
相关题目
 如图,已知AB∥CD∥EF,那么下列结论正确的是( )
如图,已知AB∥CD∥EF,那么下列结论正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下面几何体的截面图可能是圆的是( )
| A、正方体 | B、棱柱 |
| C、圆锥 | D、三棱锥 |
某商店把一件商品按进价增加20%作为定价,可是总卖不出去,后来老板把定价降低20%,以48元的价格出售,很快就卖出了,则老板卖出这件商品的盈亏情况是( )
| A、亏2元 | B、亏4元 |
| C、赚4元, | D、不亏不赚 |
 阅读理解并填空:
阅读理解并填空: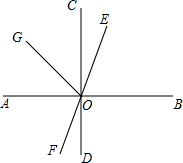 如图,已知直线AB⊥CD于O,EF过点O,OG平分∠AOE,∠FOD=28°,求∠BOE和∠AOG的度数.
如图,已知直线AB⊥CD于O,EF过点O,OG平分∠AOE,∠FOD=28°,求∠BOE和∠AOG的度数.