题目内容
12.已知△ABC的三边a,b,c满足方程组$\left\{\begin{array}{l}{2a+b=4c+1}\\{a-b=2-c}\end{array}\right.$.(1)求c的取值范围;
(2)是否存在这样a,b,c,使△ABC是等腰三角形?若存在,求出它的周长.
分析 (1)根据三角形的三边关系来求c的取值范围;
(2)需要分类讨论:a=b、b=c三种情况下的等腰三角形的周长.
解答 解:(1)$\left\{\begin{array}{l}{2a+b=4c+1①}\\{a-b=2-c②}\end{array}\right.$.
由①+②,并整理得到:a=c+1.③
由①-②×2,并整理得到:b=2c-1,④
由③+④得,a+b=3c,
所以2-c<c<3c,
解得 1<c≤2.
(2)存在这样的a,b,c,使△ABC是等腰三角形.理由如下:
当a=b时,c+1=2c-1,此时c=2,符合题意.
所以 a=b=3,
则该三角形的周长为:3+3+2=8.
当b=c时,c=2c-1,此时c=1,不符合题意;
所以存在这样的a,b,c,使△ABC是等腰三角形,且该三角形的周长为8.
点评 本题考查了三元一次方程组.解题时,需要考虑三角形的三边关系,还要注意a-b≥0这一条件.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
20.为了反映某种股票的涨跌情况,应选择( )
| A. | 扇形统计图 | B. | 条形统计图 | C. | 折线统计图 | D. | 以上三种都一样 |
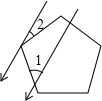 如图,一束平行太阳光照射到正五边形上,若∠1=45°,则∠2=27°.
如图,一束平行太阳光照射到正五边形上,若∠1=45°,则∠2=27°. 直线AB经过点P(3,4)与坐标轴交于A、B,当S△AOB最小时,△AOB的内切圆半径是2.
直线AB经过点P(3,4)与坐标轴交于A、B,当S△AOB最小时,△AOB的内切圆半径是2.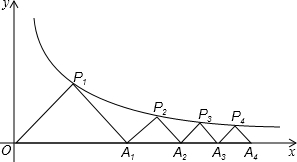 如图,△P1OA1,△P2A1A2,△P2A2A3…,是等腰直角三角形,点P1,P2,P3…在反比例函数y=$\frac{4}{x}$的图象上,斜边OA1,A1A2,A2A3…都在x轴上,则点A2的坐标是(4$\sqrt{2}$,0),A3的坐标是(4$\sqrt{3}$,0),An的坐标是(4$\sqrt{n}$,0).
如图,△P1OA1,△P2A1A2,△P2A2A3…,是等腰直角三角形,点P1,P2,P3…在反比例函数y=$\frac{4}{x}$的图象上,斜边OA1,A1A2,A2A3…都在x轴上,则点A2的坐标是(4$\sqrt{2}$,0),A3的坐标是(4$\sqrt{3}$,0),An的坐标是(4$\sqrt{n}$,0). 如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴,y轴分别交于A,B两点,∠OAB的角平分线与OB的垂直平分线相交于P点.
如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴,y轴分别交于A,B两点,∠OAB的角平分线与OB的垂直平分线相交于P点.