题目内容
已知方程x2-11x+（30+k）=0的两根都比5大，则实数k的范围是 ．
考点：根与系数的关系
专题：计算题
分析：先求出原方程的两个实数根，根据两个实数根都大于5，列出不等式组，求出k的取值范围．
解答：解：∵方程x2-11x+（30+k）=0的两根都比5大，
∴△=121-4（30+k）≥0，解得k≤
；
解方程x2-11x+（30+k）=0得x=
，
∴x1=
，x2=
，
∴
＞5，
解得k＞0，
故实数k的取值范围为：0＜k≤
．
∴△=121-4（30+k）≥0，解得k≤
| 1 |
| 4 |
解方程x2-11x+（30+k）=0得x=
11±
| ||
| 2 |
∴x1=
11+
| ||
| 2 |
11-
| ||
| 2 |
∴
11-
| ||
| 2 |
解得k＞0，
故实数k的取值范围为：0＜k≤
| 1 |
| 4 |
点评：本题考查了公式法解一元二次方程及解一元一次不等式，考查了学生的运算能力．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
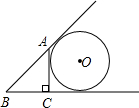如图AC⊥BC于C，BC=a，CA=b，AB=c，⊙O与直线AB、BC、AC都相切，则⊙O的半径为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
方程
=0.2可变形为（ ）
| x-0.1 |
| 0.3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
计算（-3a3）2的结果是（ ）
| A、-6a5 |
| B、6a5 |
| C、9a6 |
| D、-9a6 |
如图：设P是边长为12的正△ABC内一点，过P分别作三条边BC、CA、AB的垂线，垂足分别为D、E、F．已知PD：PE：PF=1：2：3．那么，四边形BDPF的面积是用数字3、4、5、6排列成2个自然数A，B，使A×B的积最大，那么A×B=（ ）
| A、64×53 |
| B、643×5 |
| C、543×6 |
| D、63×54 |